More actions
Naara elein (talk | contribs) |
Naara elein (talk | contribs) m →General |
||
| Line 33: | Line 33: | ||
A few important things with x^a is that when a = 0, e.g. x^0, the answer will always be 1 regardless of what 'x' is. In this case 1 corresponds to 100%, that is 100% hit chance. When a = 1, we get x^1 which is the same as 'x', in the to hit equation a power of 1 means 0.5^1 = 0.5, so a 50% hit chance. If 'a' is very high instead, the answer will approach 0, for all practical purposes it will be a 0% hit chance. So what does all this mean? It means that we want 'a' (the big scary thing on the upper right side of 0.5 in the equation above) to be as small as possible to have a high chance of hitting a target. Alternatively, we might want a foe to have an 'a' that is as large as possible to reduce his damage output. | A few important things with x^a is that when a = 0, e.g. x^0, the answer will always be 1 regardless of what 'x' is. In this case 1 corresponds to 100%, that is 100% hit chance. When a = 1, we get x^1 which is the same as 'x', in the to hit equation a power of 1 means 0.5^1 = 0.5, so a 50% hit chance. If 'a' is very high instead, the answer will approach 0, for all practical purposes it will be a 0% hit chance. So what does all this mean? It means that we want 'a' (the big scary thing on the upper right side of 0.5 in the equation above) to be as small as possible to have a high chance of hitting a target. Alternatively, we might want a foe to have an 'a' that is as large as possible to reduce his damage output. | ||
If you thought this part was tricky, don't worry about it, its not like anyone will ever solve equations like this when playing. We will now look into how this effect gameplay | If you thought this part was tricky, don't worry about it, its not like anyone will ever solve equations like this when playing. We will now look into how this effect the gameplay. | ||
==Range== | ==Range== | ||
Revision as of 10:40, 5 September 2010
This article looks into the equations and math behind gunnery. Both to see how it really works and also to see what effect it has on the outgoing DPS (damage per second). There will be plenty of math and graphs, but the text will carefully explain how it works and examples will be used often. Hopefully this will allow the reader to better judge the effects from fighting in falloff and how to determine just how important tracking is against a fast moving ship.
Governing Equation
- Transversal speed = Movement up/down/left/right relative to an object, but not towards or away from it (that is called radial speed). Measured in m/s.
- Range to target = The range to an object. Measured in meters.
- Turret tracking = Found on the attributes tab of a turret. Measured in rad/second.
- Turret signature resolution = Higher values make it harder to hit small signature radii. Measured in meters.
- Target signature radius = The size of the target, or more precisly the radius of an imagined circle that represents the target's sensor footprint. Measured in meters.
- max(0, x) = Takes the highest value of zero or x. Used to set all negative values to zero in this case.
- Turret optimal range = Found on the attributes tab of a turret. Inside this range no range penalites from distance are applied. Measured in meters.
- Falloff = Found on the attributes tab of a turret. Represents how rapidly a turret's accuracy declines as the target moves beyond optimal range. Measured in meters.
This equation can look a bit intimidating at first. But it is central to the way turrets deal damage, because it calculates each turret's chance to hit its target, so its a good idea to take a good look at it and see what can be learned from it. In the rest of this article this equation will be poked, prodded and picked apart until all its secrets are belong to us. First of all: by looking at the different variables in the equation above, we can see that many of them are fixed or require certain modules to manipulate, e.g signature radius. In an unfitted ship, the only variables that a pilot have any control over are range to target and transversal speed. All the other variables can only be manipulated by fitting in a certain way or by activating certain fitted modules. Let's look a little closer at the equation and see what more we can learn.
To paraphrase Oli Geist, this equation can be abstracted to:
Chance to hit = 0.5 ^ (tracking term + range term).
Those who know a bit of math will recognize that x^(a+b) is the same as (x^a)*(x^b), so this can also be written as:
Chance to hit = 0.5 ^ (tracking term) * 0.5 ^ (range term)
From this we can see that tracking and range are calculated seperately and are then multiplied. So anything that effects range does not effect tracking. In other words, excellent tracking can not make up for a range problem, and vice versa.
General
What does an expression like x^a mean? Just in case you are not familiar with this kind of math, lets take a look at some basics. Its read as 'x to the power of a' and is nothing more than a convenient way of writing 'x' times itself 'a' number of times, if x = 0.5 and a = 3 this will be 0.5*0.5*0.5, so 0.5 multiplied with itself 3 times. That is easy enough. Things become a little more abstract when 'a' has decimals or is lower than 1, e.g. 0.5^(0.3), how does one multiply 0.5 with itself 0.3 times? The interested readers will have to look up the answer to that elsewhere, since its not required to know that to continue reading.
A few important things with x^a is that when a = 0, e.g. x^0, the answer will always be 1 regardless of what 'x' is. In this case 1 corresponds to 100%, that is 100% hit chance. When a = 1, we get x^1 which is the same as 'x', in the to hit equation a power of 1 means 0.5^1 = 0.5, so a 50% hit chance. If 'a' is very high instead, the answer will approach 0, for all practical purposes it will be a 0% hit chance. So what does all this mean? It means that we want 'a' (the big scary thing on the upper right side of 0.5 in the equation above) to be as small as possible to have a high chance of hitting a target. Alternatively, we might want a foe to have an 'a' that is as large as possible to reduce his damage output.
If you thought this part was tricky, don't worry about it, its not like anyone will ever solve equations like this when playing. We will now look into how this effect the gameplay.
Range
So what can we do to maximize hits? Well, the range term becomes zero if we're at or under our turret's optimal range. It goes to 1 at (optimal + falloff), to 4 at (optimal + 2* falloff), and to 9 at (optimal + 3* falloff). 0.5^4 is 0.0625, or a 6.25% chance of hitting a large stationary target at that range. 0.5^9 is 0.002, or a 2/1000 chance of hitting -- good luck with that!
So we can say that any range over (optimal + falloff) is very sketchy, and staying at or near optimal range is good. No surprises here.
Tracking
What about tracking? Well, if the transversal speed is 0, the tracking term evaluates to zero (multiply with a zero and the answer is always zero). Since 0.5^0 = 1, this means that the tracking part of the equation will give a 100% hit chance, and as long as the target stays inside optimal range the chance to hit will remain at 100%. It doesn't matter if you are in a tiny frigate and your foe uses capital ship guns, your small size means nothing if your transversal is zero. This is not how things work in real life, but it is how EVE works. So getting your target to fly straight towards you, or straight away from you, is great, if you are the one with the big guns. If the target instead makes sure to keep up their transversal speed they will be harder to hit. The best way to minimize the tracking term is some combination of:
- Keep the target at longer range
- Lower the transversal speed
- Increase your turret's tracking speed and/or decrease its signature resolution
- Increase the target's signature radius
Modules that can help with these are AB's/MWD's, webs, tracking computers, and target painters. You can also choose 'keep at range' on a target to minimize the transversal (note: not verified, must be looked into) -- though bear in mind that your target will be able to hit you more easily too. Note also that if the range ever becomes zero, the equation makes a forbidden division with zero. This results in an error and the turrets will automatically miss.
Turret damage output
Base damage
A turret's base damage is a fixed number, calculated by multiplying the turrets damage multiplier (make sure it's fitted, and that you are in the ship before looking up the value to get all bonuses included -- you can also check this in EFT) and the sum of the damage types from the loaded ammo type. The target's resistance values are not taken into consideration. The base damage is a tad below the average damage (about 1.5% lower) when there is a 100% hit chance -- the reason for this are the perfect hits.
Example: A turret has a damage multiplier of x1.725, and is loaded with an ammo type that does 7 EM and 5 Thermal damage. The base damage is then 1.725*(7+5) = 20.7
Random damage distribution
At the heart of a turret's damage output is a single randomly generated value between 0 and 1 that is several digits long, something like 0.317226. This random number is used both to determine if the turret hits the target and then to determine how much damage the hit actually did. Should the randomly generated number be less than 0.01 (1% chance), it will be a perfect hit (aka 'wrecking'). A wrecking hit always deals exactly three times the base damage. The thing about perfect hits is that they always occur as long as that random number was lower than 0.01 and at the same time lower than the hit chance. So perfect hits are not scored by 1% of the shots that can hit, but by 1% of all hits and misses taken together. This means that if your chance to hit is 1% or below, you can only get perfect hits and misses. Almost all shots will miss of course, but those that do hit they will be perfect.
The raw damage dealt by a turret is calculated by taking the randomly generated number that resulted in a hit, adding 0.49, and multiplying this sum with the turret's base damage. Since the first 0.01% of the random value is used for perfect hits, the random values that hit normally are those between 0.01 and up to 1 at most (1 if the chance to hit is 100%). So if the chance to hit was 100%, this means that the normal damage will be between 50% (0.01+0.49) and 149% (1+0.49) of the base damage, or in the case of perfect hits always exactly 300% of the base damage. This number will then be reduced accordingly by the target's damage resistances in order to obtain the final damage number.
- Damage generation
- Calculating variables
- Turret Base Damage = Turret Damage Multiplier * Sum of Ammo Damages
- Hit Chance = ((calculated by the big equation at the top of this page))
- X = Random (0 to 1)
- Calculating raw damage
- If (X < 0.01 and X < Hit Chance) Then RAW DAMAGE = 3 * Turret Base Damage (these are called perfect or wrecking hits)
- Else If (X < Hit Chance) Then RAW DAMAGE = (X + 0.49) * Turret Base Damage (these are normal hits)
- Else RAW DAMAGE = 0 (these are misses)
- Calculating damage after resistance
- Resistance modified EM Damage = Ammo EM damage * (100% - Target EM Resistance)
- Resistance modified Thermal Damage = Ammo Thermal damage * (100% - Target Thermal Resistance)
- Resistance modified Kinetic Damage = Ammo Kinetic damage * (100% - Target Kinetic Resistance)
- Resistance modified Explosive Damage = Ammo Explosive damage * (100% - Target Explosive Resistance)
- Damage dealt = RAW DAMAGE * (Sum of Resistance modified damages) / (Sum of Ammo Damages)
- Calculating variables
The quality of the hit will be described by the value of the random number + 0.49, ranging from barely scratching (least damage) to excellent (highest damage) for regular hits, on top of which there may also perfect hits and misses. On the normal hits this number is multiplied with the turret's base damage. By looking carefully at the damage generation above, it becomes clear that the Hit Chance not only means that a turret can miss, it also places a cap on the maximum damage number on the non-perfect hits. The next section will deal with this in more detail.
| Hit description | Random damage modifier | |
| Perfectly | 0.490 to 0.500 (special case, 3x the base damage instead) | |
| Barely scratches | 0.500 to 0.625 | |
| Hits lightly | 0.625 to 0.750 | |
| Hits | 0.750 to 1.000 | |
| Well aimed | 1.000 to 1.250 | |
| Excellent | 1.250 to 1.490 |
A turret with a 100% hit chance will see a natural and unavoidable damage spread between 50%-149% of its base damage for normal hits, and will always do exactly 300% of its base damage on perfect hits. A turret with a 75% hit chance will have a damage spread of 50%-124% on normal hits and do 300% on perfect hits, thus it can never do any excellent hits.
Example: A turret fires on target. The chance to hit is 0.8981. The EVE server rolls a random number between 0 and 1, and gets 0.6573 -- this is less than the chance to hit so the shot lands on the target. At this point 0.49 is added to the random number which then becomes 1.1473. The turret had a damage multiplier of x2.1 and the ammo does 4 EM and 2 Thermal, so the base damage is 2.1 multiplied with 6 (4+2), which is 12.6. After multiplying this with the random number we get the raw damage, which is 1.1473 x 12.6 = 14.456. In this damage the raw EM part is 1.1473 x 2.1 x 4 = 9.6373 and the raw Thermal part is 4.8187 (half of EM). Assuming the target's shield was hit, and that only the normal 20% resistance to Thermal is in effect, the final damage then becomes 9.6373 + (4.8187*(100%-20%)) = 13.492 points. In the combat log the hit will be described as 'well aimed' and be rounded off to one decimal place.
Damage and DPS reduction due to a decreased hit chance
When a turret has less than 100% chance to hit its damage dealing capabilites are reduced in two different ways. The first and obvious one is that it sometimes misses, the other is that the max damage on normal hits (e.g. not perfect ones) is reduced as well. Both of these effects will decrease the DPS output. If you read the previous section, you may remember that the a random number between 0 and 1 is generated to see if a turret hits. If this value is lower than the chance to hit, the shot lands and this number is then used further: 0.49 is added to it, and the result is then multiplied with the turret's base damage to obtain the raw damage done (damage before resistances)
What this all means is that targets that are tricky to hit also take less damage since high rolls now are discarded as misses. This can be seen in the damage log: a hard-to-hit target never recieves excellent or well aimed hits, sometimes barely scratching is the highest possible (though of course perfect hits can still happen). The practical effect is that the DPS decreases more than the chance to hit does.
Example: (please note that perfect hits are not considered in this example to make the numbers easier to follow) A turret has 50% chance to hit at optimal+falloff, ignoring tracking. The highest randomly rolled number that can result in a hit is thus 0.5 -- higher numbers mean a miss. This will shrink the damage interval down to 0.5 to 0.99 for normal hits, which on average is 0.745 ((0.5+0.99)/2). Compare that with a case inside optimal range where the chance to hit is 100%, ignoring tracking. Here the damage interval is 0.5 to 1.49 and the average is 0.995. At optimal+falloff (and ignoring perfect hits) the DPS from normal hits are hence reduced to 50% x 0.745=37.25% of normal. (When perfect hits are taken into consideration the DPS value becomes 39.5% instead, see the table below)
The table below shows how DPS decreases as a target becomes harder to hit. Note that the reason for the hit chance reduction doesn't matter, be it because of falloff or just tracking issues, the DPS goes down identically. The table can be used to see both how the damage declines as one goes deeper into falloff, and how the damage declines as a result of a lowered hit chance due to tracking problems. If you wish to combine the effects of tracking and falloff, you can do this by first picking the hit chance from falloff and then the hit chance from tracking, multipling the values to get the combined hit chance, looking in the hit chance column until you find a hit chance that is closest to the product you got, and then reading your relative DPS from that line.
Comment: The relative DPS below is over 1 at the start, but this is not an error. It's because it's relative to the base damage of the turret. What puts it above 1 are the perfect hits, since they do extra high damage.
| Parts into falloff | Hit chance | Relative DPS | Reduction in DPS by % | |
| 0 | 1,0000 | 1,0151 | 0,0% | |
| 0,1 | 0,9931 | 1,0048 | -1,0% | |
| 0,2 | 0,9727 | 0,9747 | -4,0% | |
| 0,3 | 0,9395 | 0,9268 | -8,7% | |
| 0,4 | 0,8950 | 0,8641 | -14,9% | |
| 0,5 | 0,8409 | 0,7906 | -22,1% | |
| 0,6 | 0,7792 | 0,7104 | -30,0% | |
| 0,7 | 0,7120 | 0,6274 | -38,2% | |
| 0,8 | 0,6417 | 0,5454 | -46,3% | |
| 0,9 | 0,5704 | 0,4672 | -54,0% | |
| 1 | 0,5000 | 0,3951 | -61,1% | |
| 1,1 | 0,4323 | 0,3303 | -67,5% | |
| 1,2 | 0,3686 | 0,2736 | -73,0% | |
| 1,3 | 0,3099 | 0,2249 | -77,8% | |
| 1,4 | 0,2570 | 0,1840 | -81,9% | |
| 1,5 | 0,2102 | 0,1502 | -85,2% | |
| 1,6 | 0,1696 | 0,1225 | -87,9% | |
| 1,7 | 0,1349 | 0,1003 | -90,1% | |
| 1,8 | 0,1058 | 0,0825 | -91,9% | |
| 1,9 | 0,0819 | 0,0685 | -93,2% | |
| 2 | 0,0625 | 0,0576 | -94,3% | |
| 2,1 | 0,0470 | 0,0492 | -95,2% | |
| 2,2 | 0,0349 | 0,0428 | -95,8% | |
| 2,3 | 0,0256 | 0,0379 | -96,3% | |
| 2,4 | 0,0185 | 0,0343 | -96,6% | |
| 2,5 | 0,0131 | 0,0316 | -96,9% | |
| 2,6 | 0,0092 | 0,0277 | -97,3% | |
| 2,7 | 0,0064 | 0,0192 | -98,1% | |
| 2,8 | 0,0044 | 0,0131 | -98,7% |
The formulas used to calculate this table were:
- Chance to Hit: 0.5^(0+(Falloff parts / 1)^2)
- Relative DPS: if(HitChance>0.01 then (HitChance-0.01)*((0.50)+(HitChance+0.49))/2+0.01*3 else HitChance*3)
- Reduction in DPS: (RelativeDPSatCurrent/RelativeDPSat100%hit)*100%-100%
Damage and DPS dependancy on tracking in fast ship dogfights
(not finished)
Ammo choice and DPS in falloff
(this part might be removed, not sure of its practical value but maybe someone is interested, the math hasn't been well explained so it can be tricky to both understand and apply)
This part is about finding the highest DPS by picking the right ammo type. The only ones this particular part applies to are those who fight outside optimal ranges. Such as Blasters and Artillery. Its not relevant to anyone who anyone who uses Lasers.
Since the hard hitting ammo also have shorter optimal ranges they will be penalized harder as the distance increases. At some point the penalty becomes too big and make a longer range but lower damage ammo better for DPS. It is possible to calculate up to what falloff a hard hitting ammo will better or equal to another ammo type. The tricky part is that both kinds of ammo will end up being in falloff and the damage penalty on each must be considered. So this part is a little tricky and is something to do when inside a station and thinking about what ammo to use. It will require a few calculations, but only multiplication and division, to get numbers that are required to correctly read the graph for this part.
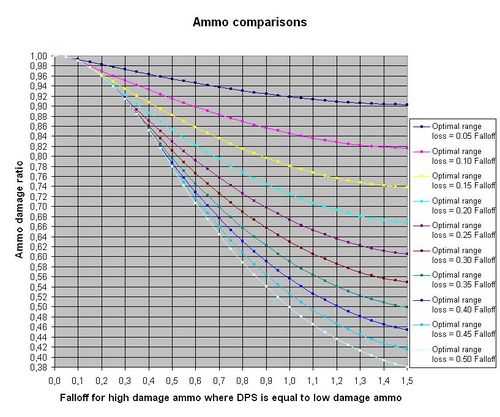
- Pre calculations
- Loss of optimal range with hard hitting ammo (measured in parts of its falloff):
- (Longer ammo % range modifier - Shorter ammo % range modifier) * Normal optimal on the turret / Falloff
- Use this number to pick the correct line to look at in the graph, if this number becomes 0.10 then use the 0.10 line in the graph, otherwise pick the closest one or if you are uncertain the go with the line that has a higher number than your ratio. The optimal range is the same one that would be obtained with standard ammo (no range modifier) but with all skill and ship modifiers included.
- Damage differance between the two ammo types:
- Total damage on longer range ammo / Total damage on shorter range ammo
- This value will be used on the left axis (the Y-axis), follow it until it meets the line you picked from the first calculation. When they meet, go straight down and read the number on the bottom axis (the X-axis). This value is the falloff multiplier where the two ammo types do the same DPS, to the left the harder hitting does more DPS and to the right the softer hitting ammo do more DPS.
Example: A blaster Brutix is using medium T2 neutron blasters. Several fights have been fought at 5-6 km distance and the pilot wonders what ammo type would be best for DPS at that range (Note: fictive example, the author haven't fought in medium blaster boats and doesn't know anything about common ranges). The Brutix have no range bonuses, with sharpshooter IV the optimal range becomes 4320m and with Trejectory Analysis the falloff becomes 6000m. Navy antimatter does 27.6 damage and navy plutonium does 25.3 damage in total. First the pilot calculate what line in the graph to look at, ((-37.5%) - (-50%)) * 4320 / 6000 = 0.125 * 4320 / 6000 = 0.09, so the 0.10 line will be the one to look at. Next he calculates the damage ratio between the ammo types, 25.3 / 27.6 = 0.9167, rounded of to 0.92. The pilot looks up 0.92 on the Y-axis and follows it towards the right until it crosses the 0.10 line, which happens at about 0.5 falloff. This would be the falloff value for the hard hitting ammo (navy antimatter) at which point it does the same DPS as the softer hitting ammo (navy plutonium), at shorter falloffs the antimatter does more DPS and at higher falloffs the plutonium does more DPS. The pilot checks what distance corresponds to 0.5 falloff for the navy antimatter ammo, that is (4320 * (100% - 50%) + 6000 * 0.5 = 5160 meters. So above 5100 meter the navy plutonium is actually a bit better. The pilot repeats an identical calculation for navy uranium and see that it does more DPS than navy plutonium over 6000 meter. The pilot decides to go with the navy plutonium.
(Note: The DPS differance in this example turns out to be small, only about 0-2% more DPS for plutonium (up to 6000m), that must be weighted to the 8.5% damage differance that happens inside optimal but also the additonal % differance at longer ranges, it all depends on what kind of ranges that is seen in actual combat).
Example 2: A minmatar Maelstrom (a battleship) is using large artillery, 1200mm Heavy Prototype I Siege Cannons. With skills the optimal is 42.58 km and the falloff is 40.25 km. The pilot is doing missions and fighting Angels, and wants to do explosive and kinetic damage. He also wants to know at what range different ammos would be best at. He picks Titanium Sabot L (8 expl, 24 kin, 0% range mod) and Fusion L (40 expl, 8 kin, -50% range mod). First the pilot calculates what line in the graph to follow: (0% - (-50%)) * 42.58 / 40.25 = 0.5 * 42.58 / 40.25 = 0.53. There is a line for 0.50 so the pilot picks that one. Since he is not sure about exact resistances for Angels, he decides to not adjust the total damage numbers to account for that, he takes them as they are and calculate the ratio between the total damage: 32 / 48 = 0.67. He looks up 0.67 on the Y-axis and looks for the intersection with the 0.50 line, it happens at 0.65 falloff. So when the harder hitting ammo is 0.65 into falloff it will deal the same kind of damage as the softer hitting one (resistance differance unaccounted for). 0.65 falloff for the hard hitting ammo (Fusion L) corresponds to a range of 42.58 * (100% - 50%) + 40.25 * 0.65 = 47.5 km.
Answers to some questions
Do small targets take less damage from big guns?
Yes, if it has a transversal speed. Since big guns have large signature resolution values and low tracking values, it becomes harder to hit a small and fast target. The lowered hit chance is what reduces the damage, nothing else. The lowered hit chance results both in less DPS and lower maximum damage (not counting perfect hits, they always do the same damage). If the transversal speed is zero on the other hand, and the small ship inside optimal range, then it will take the full damage and be hit by every shot.
Can a turret hit a target with a larger angular velocity than its own tracking?
Yes it can. From the chance to hit equation it can be deduced that the tracking part can be broken down into):
Chance to hit (tracking part) = 0.5 ^ (((Angular velocity / Turret tracking) * (Size ratio between gun and target))^2)
We will assume that the target is inside optimal for the rest of this question, so that we can ignore the additional loss of hit chance if the target was in the falloff, if you wish to compensate for a target in falloff simply multiply the hit chance from the range part with the hit chance from the tracking part to get overall chance to hit.
From the equation above it can be seen that the angular velocity (= transversal speed / range to target) and the turret tracking are compared as a ratio -- it's not an upper limit. So turrets with less tracking than their target's angular velocity can still hit: all that happens is that the chance to hit is reduced. If we consider a case in which angular velocity is equal to the turret's tracking, and assuming that the size ratio between gun and target is 1 (the gun's signature resolution is equal to the targets signature radius), we get chance to hit = 0.5^((1/1*1)^2) = 0.5^1 = 0.5, or 50%. So, roughly speaking a gun will hit 50% of the time when angular velocity and turret tracking are the same on same sized targets.
If the angular velocity is twice as high as the tracking (and gun and ship still have identical sizes), the chance to hit becomes 0.5^4 = 6.25%. If the tracking is twice as big as the angular velocity (and again, size ratio is 1) then the chance to hit will be 0.5^((0.5)^2) = 0.5^0.25 = 84.1%. In theory small and fast ships could benefit more from tracking bonuses than they would from raw damage bonuses, at least if nobody tries any clever manual piloting moves.
Are frigates with a smaller signature radius better than larger frigates in frigate pvp?
When comparing small signature radii, say 35m and 43m, the differance is only noticeable at short distances (up to 1 or 2 km). The one with the smallest radius get a small advantage from this factor. However, other factors come into play as well, and this advantage is many times offset by the fact that the larger-signature frigates use guns that generally have higher tracking values (the trend is: projectiles have the worst tracking, lasers are in between, hybrids have the best; when compared on an equal basis). So it really doesn't seem to matter. What is clear is that a high tracking can be more important than the damage multiplier on the gun, especially since the max damage drops if the gun can't track well enough.
Are target painters useful for turrets?
Yes, but only if the chance to hit is below 100% due to the tracking part of the Hit Chance equation. If the decreased hit chance is because of range then a target painter will not help at all, even though one might think so.
A regular Target Painter I increases the signature radius of a ship by +25%. Since all tracking terms are multiplied with another in the hit chance equation, the number can be moved around inside it to see how it effects the other factors. So another way to look at it is this: the signature radius increase is identical to what would happen if the target instead had reduced its angular velocity to 80% (100%/125%) of its current or as if the turrets had gotten +25% more tracking against the target. (Keep in mind that this last part was only a comparison, a target painter doesn't actually reduce anyone's speed or improves anyone's tracking.)
If I group my guns, does EVE pick the same random number for all of them?
No. Even if the guns are grouped on your screen, they are still treated separately. This can be seen by collecting damage data and comparing that with the normal expected damage distribution, its very clear that its a combination of several seperate turret shots. It can also be deduced by looking at the turret group's damage output when shooting at hard to hit objects, like deep into falloff, its quite easy to tell when one, two or more guns hit the target.
+0.49? It says +0.50 on EVEonline wiki
Yes it does and the differance isn't exactly overwhelming. But the test that was made to ensure the validity of this article showed a small deviance. The test has too much collected data to present all of it here, so the method and results will be presented instead. Should you wish to check for yourself feel free to follow this procedure.
A frigate (named 'Ouch') was abandoned at a safespot. An Osprey was fitted with lasers (infinite ammo, perfect for afk:ing), a remote shield transfer and shield transfer drones. The guns and the ammo were chosen so that the damage would never go below 10.0 and to give as large of a damage interval as possible (an interval of at least 10.0 units (resistances must be accounted for) is needed to get a precision of at least 1% in the damage values) -- this ensured that the data would be good enough to draw accurate conclusions. The damage was only done to the shields, they where never allowed to drop below 25% since a bleed through into armor can happen that can mess with the observed damage numbers. Finally, the ships were positioned within optimal range and their speeds set to zero to ensure that the chance to hit is 0.5^0 = 100% and nothing less.
After 10,656 shots at the poor frigate, enough data was collected to make some conclusions about how the random damage distribution looks like. The data ends up in the My Documents\EVE\gamelogs folder (in Windows), and was easily copied into a prepared Excel sheet for analysis.
- Base damage
- The ammo type dealt: 7 EM and 5 Thermal
- The base damage on the lasers were: 24.9063
- Compensating for resistance (20% thermal) the modified base damage is: 22.8308
Analysis of the data and interpretation of some reduced frequencies of min and max results in the normal damage span:
Of the 10,656 shots the lowest recorded damage was 11.4 (recorded 15 times) and the highest non-perfect was 34.0 (recorded 33 times), perfect hits dealt 68.5 damage (recorded 101 times). On average, each damage number (anything between 11.5 to 33.9) was recorded 46.7 times (standard deviation = 7.02). The reason for the lower occurences of the min and max results on normal hits comes from rounding effects. Any damage in-between has an interval of 0.1 units (22.2500 to 22.3499 both produce the 22.3 in the log). However the min and max values do not have that span. The lowest theoretical number is Base Damage x 0.5 = 11.415, hence the interval to get 11.4 in the log is between 11.415 and 11.4499, that is only 0.0345 differance. So the expected number of occurances of the value 11.4 is only 34.6% of the average number, 15 recorded values / 34.6% = 43.4, close to average and inside the standard deviation. The upper interval is 67.8%, 33 times / 67.8% = 48.7, also close to average and inside the standard deviation. (Note: 34.6%+67.8%=102.4%, which is of course impossible -- the error comes from rounding errors in the 4th decimal of the base damage, awesome precision isn't needed for this comparative calculation since the natural random deviation is much larger anyhow, so this is good enough, the objective was to explain the lower frequencies of the end points which now has been done).
- Lowest damage random multiple
- Modified base damage x 0.51 = 11.6
- Modified base damage x 0.50 = 11.4
- Modified base damage x 0.49 = 11.2
- The lowest observed damage is 50%
- Highest non-perfect random multiple
- Modified base damage x 1.50 = 34.2
- Modified base damage x 1.49 = 34.0
- Modified base damage x 1.48 = 33.8
- The highest non-perfect damage is 149%
- Perfect hits deal 68.5 damage
- Modified base damage x 3 = 68.5
The collected data shows that the normal damage is distributed within 50%-149%. Since the first 1% unit is used for critical rolls, this means that the constant has to be 0.49.
Tracking Examples
coming soon
References:
http://wiki.eveonline.com/wiki/Turret_damage
http://www.eve-ivy.com/forum/viewtopic.php?p=201888#201888
http://www.eve-ivy.com/forums/viewtopic.php?p=216525#p216525

