This is the personal draft space for elaborating the idea. Any suggestion is highly appreciated!
Widget will be available on github or something...
Note: On this page, the terms "orbiting speed" and "orbiting velocity" are used interchangeably. They both refer to the target’s movement speed along its orbital path. Also, the term "stationary" is used instead of "static" to more accurately describe ships that are not moving.
Visualization formula derivation
It is recommended to read the Turret_mechanics#Hit_chance section beforehand, as this explanation assumes a basic understanding of turret mechanics.
According to the hit chance formula, we have:
To visualize this complex formula intuitively, we apply the following constraints to simplify the setup:
- The attacker is stationary.[Note 1]
- The target is either stationary or moving in a perfect circular orbit around the attacker.
- The scenario takes place on a 2D plane.[Note 2]
First, consider the distance term.
This term shows that hit chance decreases the further the target is beyond optimal range. This relationship can be visualized along a 1D axis.
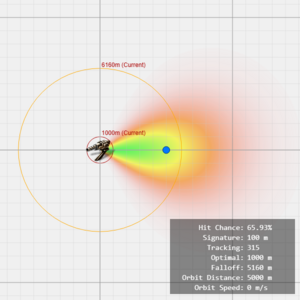
Note that the orbiting velocity (orange arrow arc) lies within the yellow area of the heatmap, which represents mediocre hit chance.
Next, consider the tracking term:
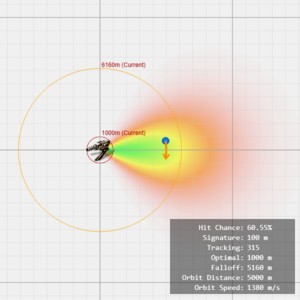
We can visualize the target's orbiting motion as an arc. The length of this arc over one second represents the target’s orbital velocity. For a given orbital velocity, the angular velocity (how quickly the target moves across the turret’s aim) increases as the orbital radius (distance to the attacker) decreases:
This means, the closer the target is while orbiting at the same speed, the harder it is for the turret to track.
From this, we can interpret the turret's tracking stat as a kind of "maximum allowable angular velocity" it can handle. Visually, this forms a 2D cone shape where hit chance remains high within the cone and falls off outside of it.
By combining the 1D distance-based falloff term with the 2D angular velocity-based tracking cone, we can visualize the hit chance on a 2D plane using a heatmap.
Visualized comparison
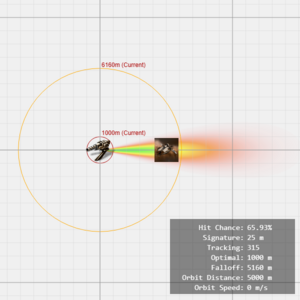
Different turret types have different property. The following three figures shows the property of each turrets, when targeting against a stationary object of 100 signature radius at 5000m distance.
For example, autocannons have a very short optimal range and long falloff, thus having a bigger yellow to orange area. Pulse lasers have long optimal and short falloff, and the worst tracking, which results in long but narrow cone of green area. Blasters have the best tracking but worst range, showed by the short and wide cone.
|
|
|
|
|---|
|
|
|
|
|---|
Title 3
Some more description...
Some more description...
Some more description...