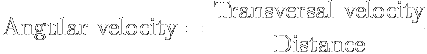More actions
Just wanted to add a practical meaning section, providing two examples as to how these three velocities relate to Eve movement. |
m Remove category |
||
| Line 1: | Line 1: | ||
{{New Work in Progress}} | {{New Work in Progress}} | ||
This page will explain the meaning of three kinds of variables related to velocity. Velocity itself can be described as the vector, i.e. both a magnitude (speed) and direction, by which an object in motion moves. In EVE, velocity is almost always in units of meters per second (m/s). This is often displayed as a scalar quantity, which can be misleading or confusing since they really mean speed in most cases. For the purposes of EVE, we will relax this formalism to aid in understanding and simply say that '''velocity is the speed of an object'''. | |||
This | |||
It is important to note that radial, transversal, and angular velocity are the same for both you and an object. For example, if you have a transversal velocity of 500 m/s with respect to another player's ship, then he also has a 500 m/s transversal velocity with respect to your ship. | It is important to note that radial, transversal, and angular velocity are the same for both you and an object. For example, if you have a transversal velocity of 500 m/s with respect to another player's ship, then he also has a 500 m/s transversal velocity with respect to your ship. | ||
== Radial Velocity == | |||
Radial velocity describes in EVE the speed at which the distance between you and the object changes. If the distance between you and the object increases, then the value is positive. If the distance between you and the object decreases, then the value is negative. In other words, as you move toward the object, both you and it have a negative radial velocity. | Radial velocity describes in EVE the speed at which the distance between you and the object changes. If the distance between you and the object increases, then the value is positive. If the distance between you and the object decreases, then the value is negative. In other words, as you move toward the object, both you and it have a negative radial velocity. | ||
| Line 14: | Line 10: | ||
Just to provide another explanation, consider a sphere centered at your ship so that the object is on the surface of the sphere. As you and the object move around, the sphere follows you and also adjusts its size. The speed at which the sphere's size changes is determined by its radius, hence the term "radial" velocity. | Just to provide another explanation, consider a sphere centered at your ship so that the object is on the surface of the sphere. As you and the object move around, the sphere follows you and also adjusts its size. The speed at which the sphere's size changes is determined by its radius, hence the term "radial" velocity. | ||
== Transversal Velocity == | |||
Transversal velocity in EVE describes the speed at which an object moves perpendicular to you, i.e. its orbital velocity. In other words, it is a metric used to describe the sideways movement of you and an object relative to one another. To get an sense of what this means, below is a list of some examples. | Transversal velocity in EVE describes the speed at which an object moves perpendicular to you, i.e. its orbital velocity. In other words, it is a metric used to describe the sideways movement of you and an object relative to one another. To get an sense of what this means, below is a list of some examples. | ||
| Line 30: | Line 26: | ||
The transversal velocity is computed by subtracting the two velocity vectors (i.e. both magnitude and direction) from one another, and then finding the length of the vector. This differs from angular velocity (below) in that it is not affected by the distance between both objects. | The transversal velocity is computed by subtracting the two velocity vectors (i.e. both magnitude and direction) from one another, and then finding the length of the vector. This differs from angular velocity (below) in that it is not affected by the distance between both objects. | ||
== Angular Velocity == | |||
Angular velocity describes in EVE the speed at which you and an object rotate around each other. It is measured in radians per second. For example, if you have an angular velocity at 6.283 rad/sec, then you are orbiting a full circle every second (since 6.283 = 2 * PI). Angular velocity has a very important relationship with transversal velocity. | Angular velocity describes in EVE the speed at which you and an object rotate around each other. It is measured in radians per second. For example, if you have an angular velocity at 6.283 rad/sec, then you are orbiting a full circle every second (since 6.283 = 2 * PI). Angular velocity has a very important relationship with transversal velocity. | ||
| Line 38: | Line 34: | ||
People often debate between using either transversal or angular velocity in an overview setup. Both variables display similar information; however, angular velocity is much more useful in practice, due to its use in turret to-hit calculations. It essentially allows for an easy comparison between your (or your opponent's) turret's tracking speed and the angular velocity. If the angular velocity is greater then the turret's tracking speed, you'll begin to miss, but having a smaller angular velocity than the turret's tracking speed means maximizing the hit chance. | People often debate between using either transversal or angular velocity in an overview setup. Both variables display similar information; however, angular velocity is much more useful in practice, due to its use in turret to-hit calculations. It essentially allows for an easy comparison between your (or your opponent's) turret's tracking speed and the angular velocity. If the angular velocity is greater then the turret's tracking speed, you'll begin to miss, but having a smaller angular velocity than the turret's tracking speed means maximizing the hit chance. | ||
== Practical Meaning == | |||
Due to the mechanics of [[Turret Damage]], velocity plays a large role in determining the probabilty of successfully hitting targets. Knowing how to control your shared velocity variables can be a huge advantage in a fight. For example, the reason that frigates can tackle battleships and survive is due to the relation between the high angular velocity and the battleship's turret's low tracking speeds. Also, the rate at which a ship is closing in on another is determined by its radial velocity. By balancing radial velocity with transversal/angular velocity can help you pull range or close in on a target, while still being able to survive. Next, we'll look at two expanded examples to further explain these concepts and relate it to Eve. | Due to the mechanics of [[Turret Damage]], velocity plays a large role in determining the probabilty of successfully hitting targets. Knowing how to control your shared velocity variables can be a huge advantage in a fight. For example, the reason that frigates can tackle battleships and survive is due to the relation between the high angular velocity and the battleship's turret's low tracking speeds. Also, the rate at which a ship is closing in on another is determined by its radial velocity. By balancing radial velocity with transversal/angular velocity can help you pull range or close in on a target, while still being able to survive. Next, we'll look at two expanded examples to further explain these concepts and relate it to Eve. | ||
Revision as of 07:17, 21 October 2014
Template:New Work in Progress This page will explain the meaning of three kinds of variables related to velocity. Velocity itself can be described as the vector, i.e. both a magnitude (speed) and direction, by which an object in motion moves. In EVE, velocity is almost always in units of meters per second (m/s). This is often displayed as a scalar quantity, which can be misleading or confusing since they really mean speed in most cases. For the purposes of EVE, we will relax this formalism to aid in understanding and simply say that velocity is the speed of an object.
It is important to note that radial, transversal, and angular velocity are the same for both you and an object. For example, if you have a transversal velocity of 500 m/s with respect to another player's ship, then he also has a 500 m/s transversal velocity with respect to your ship.
Radial Velocity
Radial velocity describes in EVE the speed at which the distance between you and the object changes. If the distance between you and the object increases, then the value is positive. If the distance between you and the object decreases, then the value is negative. In other words, as you move toward the object, both you and it have a negative radial velocity.
Just to provide another explanation, consider a sphere centered at your ship so that the object is on the surface of the sphere. As you and the object move around, the sphere follows you and also adjusts its size. The speed at which the sphere's size changes is determined by its radius, hence the term "radial" velocity.
Transversal Velocity
Transversal velocity in EVE describes the speed at which an object moves perpendicular to you, i.e. its orbital velocity. In other words, it is a metric used to describe the sideways movement of you and an object relative to one another. To get an sense of what this means, below is a list of some examples.
A high transversal velocity occurs when:
- Two ships orbit one another at the same speed in opposite directions (maximal transversal)
- One ship orbits a stationary ship
- One ship flies "north" and the other flies "east/west" with respect to one another
A low transversal velocity occurs when:
- Two ships fly directly away or toward one another (zero transversal)
- Two ships fly perfectly parallel to one another at the same speed (zero transversal)
- One ship chases the other ship
The transversal velocity is computed by subtracting the two velocity vectors (i.e. both magnitude and direction) from one another, and then finding the length of the vector. This differs from angular velocity (below) in that it is not affected by the distance between both objects.
Angular Velocity
Angular velocity describes in EVE the speed at which you and an object rotate around each other. It is measured in radians per second. For example, if you have an angular velocity at 6.283 rad/sec, then you are orbiting a full circle every second (since 6.283 = 2 * PI). Angular velocity has a very important relationship with transversal velocity.
People often debate between using either transversal or angular velocity in an overview setup. Both variables display similar information; however, angular velocity is much more useful in practice, due to its use in turret to-hit calculations. It essentially allows for an easy comparison between your (or your opponent's) turret's tracking speed and the angular velocity. If the angular velocity is greater then the turret's tracking speed, you'll begin to miss, but having a smaller angular velocity than the turret's tracking speed means maximizing the hit chance.
Practical Meaning
Due to the mechanics of Turret Damage, velocity plays a large role in determining the probabilty of successfully hitting targets. Knowing how to control your shared velocity variables can be a huge advantage in a fight. For example, the reason that frigates can tackle battleships and survive is due to the relation between the high angular velocity and the battleship's turret's low tracking speeds. Also, the rate at which a ship is closing in on another is determined by its radial velocity. By balancing radial velocity with transversal/angular velocity can help you pull range or close in on a target, while still being able to survive. Next, we'll look at two expanded examples to further explain these concepts and relate it to Eve.
Visually, angular velocity may be thought of as the arc, or curved line, on a sphere centered at you. For example, if you held a weight on a piece rope and began to spin in place, the rate at which you spun the weight around you is the angular velocity. In this scenario, transversal velocity would be described as the difference between your velocity (which is zero) and the weight's velocity (which points in the direction it is moving). Now consider the rope was ten times the original length. If you spun your arms at the same rate as you did before, then the speed of the weight (transversal velocity) would be ten times as fast; however, its angular velocity would remain the same. If you had instead preserved the speed of the weight as it moved from its perspective, the angular velocity would instead be one tenth the original value.
For this reason, frigates (the weight) performing a spiraling maneuver in on a turret-based battleship (the person) are attempting to keep a negative radial velocity (slowly pulling in on the rope) to move toward the battleship. So as to avoid going into the details of turret damage, we'll assume the battleship's turrets are only affected by velocities (not the case in practice). With that assumption, the frigate needs to spiral by adjusting his transversal velocity vector to ensure his angular velocity is near or above the tracking speed of the battleship's turrets. This is affected by his distance to the battleship, and as we saw in the example above, the closer the frigate (weight) is to the battleship (person), the higher is angular velocity is, even if the ships capabilities (speed) are unchanging. This is also why small turrets have higher tracking speeds and partially why webifiers on a target don't really affect a frigate's ability to hit as it orbits close. In this case, a webifier slows the battleship down so that the angular velocity decreases enough for the frigate's smaller turrets to still hit, but battleship's larger turrets to miss.
As a last example, consider two identical turret-based frigates (fitting, ship type, etc.). If both perfectly orbit one another moving 5000 m/s, then their perfectly opposite velocities will be subtracted from one another and effectively double the value to a 10000 m/s transversal (v - (-v) = 2v). This makes it harder for both of them to hit one another. Now consider the case where one of the frigates begins to manually turn itself to match the exact motions of the other, i.e. move parallel to it, instead of orbiting. In this case, their velocities will cancel out and the probability of them hitting one another will be much higher.
These are just a few examples to explain the idea of radial, transversal, and angular velocities in Eve. Please see the Advanced Piloting Techniques article for a more detailed guide on this intricate topic.