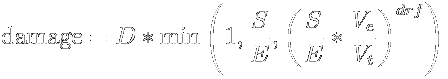This article takes a look at mathematics behind missiles. We look at the equations that govern how far your missiles will travel and how much damage they deal. There's some math at the beginning, but you can skip over this if you wish.
Missile Damage Output
First Look at the Damage Equation
Here is the equation for missile damage:
If this looks daunting, then skip ahead to read the applications of the formula to combat. Here are the terms in the equation:
- D : base damage of missile
- S : signature radius of target
- E : explosion radius of missile
- Ve: explosion velocity of missile
- Vt: velocity of target
- drf: damage reduction factor of missile
The log function used here is in base e, not base 10. You may have seen it written as ln. Note that unlike the turret damage equation, the missile damage does not care about angular velocity, but absolute velocity. To find your damage, the game computes each of the three numbers you see, picks the smallest of the, and multiplies that by the base damage. The damage reduction factor is a hidden stat, but seems to be the same for all missiles of a given size.
| Missile Type | DRF | log(DRF)/log(5.5) |
| Rocket | 3.0 | 0.644 |
| Light Missile | 2.8 | 0.604 |
| Assault Missile | 4.5 | 0.8823 |
| Heavy Missile | 3.2 | 0.6823 |
| Torpedo | 5.0 | 0.9441 |
| Cruise Missile | 4.5 | 0.8823 |
| Citadel Torpedo | 5.5 | 1.0 |
| Citadel Cruise Missile | 4.5 | 0.8823 |
Note that you want a small DRF, since smaller powers of numbers less than 1 are larger.
Explosion Velocity
Our first fact is this: if the target is moving slower than the explosion velocity of your missile, then the third term in the equation can be ignored. In this case, Ve / Vt > 1, and so S/E*(Ve / Vt) > S/E. Now, if S/E*(Ve / Vt) > 1, then taking raising it to that power will still leave it larger than 1, so we only need to consider the minimum of 1 and S/E. However, if S/E*(Ve / Vt) < 1, then applying the DRF factor will make it larger, and S/E will be smaller and we are once again left with only having to compare between 1 and S/E.
The second fact is this: just because the target is moving faster than your explosion velocity does not mean that your damage is reduced. You can show that your missile damage is reduced because of the target's velocity if and only if
That is, if the target is flying at speeds greater than the term on the right, then your damage reduction is no longer the smaller of 1 or S/E and instead becomes the smaller of 1 and the third, more complicated, number.