More actions
No edit summary |
|||
| (One intermediate revision by the same user not shown) | |||
| Line 51: | Line 51: | ||
The collected data shows that the normal damage is distributed within 50%–149%. Since the first 1% unit is used for critical rolls (this is most likely, if the last % unit was used additional calculations will be needed if the to hit chance is less than 1%), the constant added to the damage roll should be 0.49. | The collected data shows that the normal damage is distributed within 50%–149%. Since the first 1% unit is used for critical rolls (this is most likely, if the last % unit was used additional calculations will be needed if the to hit chance is less than 1%), the constant added to the damage roll should be 0.49. | ||
==Turret grouping and damage== | |||
I did a test to verify that grouping has no effect on turret damage. | |||
Shot at a ship inside optimal. Took damages for each shot from game log. Created quick histograms with MATLAB. | |||
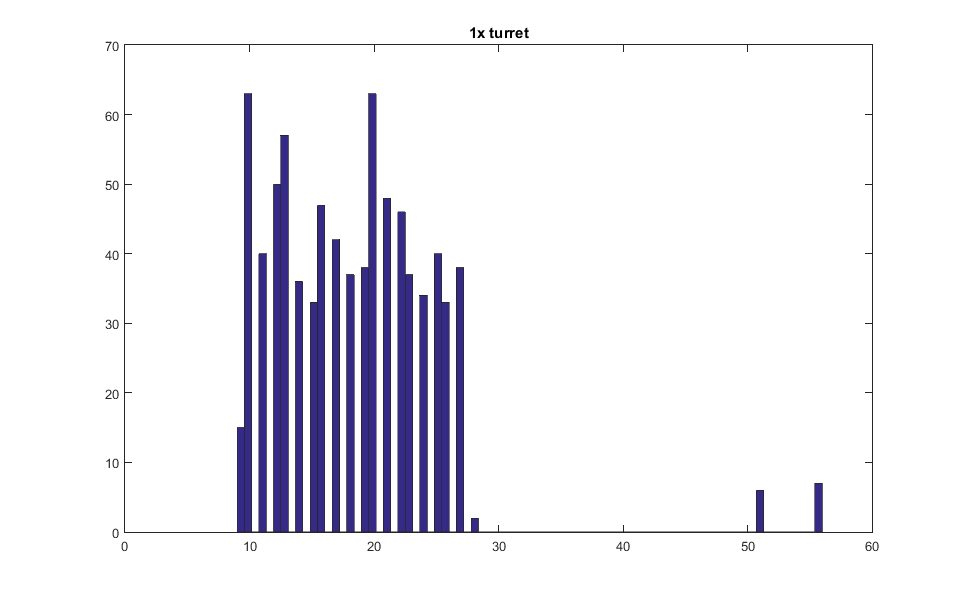
One turret has the flat distribution.<br> | |||
[[File:Damage distribution one turret.png]] | |||
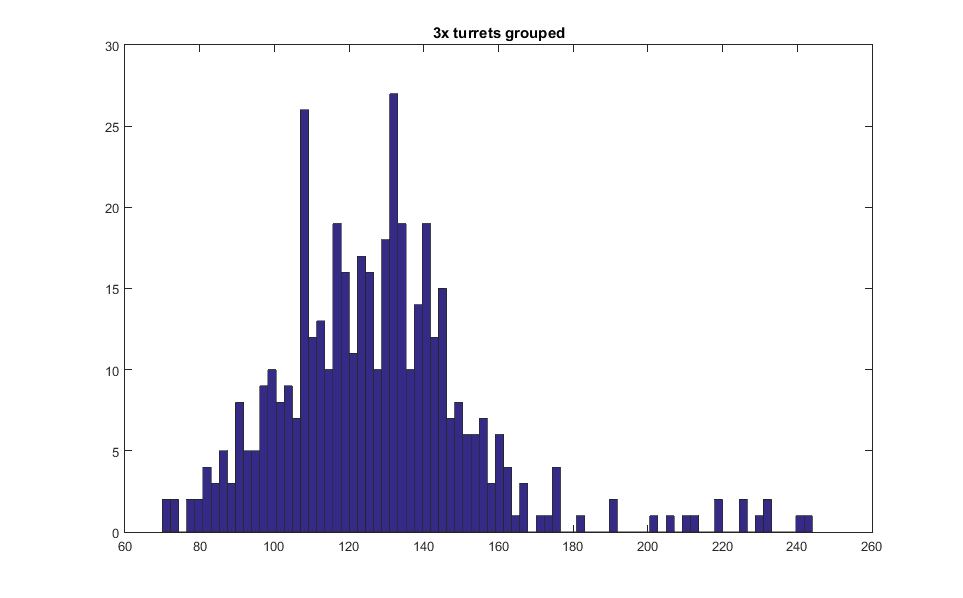
Three turrets grouped together form normal distribution. This is as expected with multiple separate random distributions together.<br> | |||
[[File:Damage distribution two turrets.png]] | |||
[[User:Hirmuolio pine|Hirmuolio pine]] ([[User talk:Hirmuolio pine|talk]]) 14:23, 19 December 2017 (CST) | |||
Latest revision as of 20:25, 19 December 2017
The idea behind this page is to present the gunnery information in Dinsdale's gunnery class in a readable and not too mathematical way.
Various helpful people in Chat.E-UNI and Command.ILN patiently explained how tracking and signature resolution work to me, repeatedly, and much of what hasn't been shamelessly plagiarised from Dinsdale is down to them. Errors and omissions (and I'm sure they exist -- please correct them) are my fault, not theirs. --Uryence 20:07, 3 April 2010 (UTC)
Damage stacking
Could there be an inclusion of information on how skills affect damage for guns.
For instance if you have advanced autocannons IIs
do the following skills apply: 1. Gunnery: I assume yes. 2. Large Projectile turrets: Yes on T1/Faction; does it apply to T2s? 3. Large Autocannon Specialization: No on T1/Faction, yes on T2?
If question 2 is no on T2s how high does 3 have to be to eclipse the T1s? (Maybe it doesn't matter due to ammo selection?
Experiment to determine the damage interval around base damage
This used to be at the end of turret damage. Moved it here so it is not lost.Hirmuolio pine (talk) 02:51, 17 December 2017 (CST)
This test has too much data to show all of it here, so the method and the results will be presented instead. Should you wish to check for yourself feel free to follow this procedure:
A frigate (named 'Ouch') was abandoned at a safespot. An Osprey was fitted with lasers (infinite ammo, perfect for AFKing), a remote shield transfer and shield transfer drones. The guns and the ammo were chosen so that the damage would never go below 10.0 and to give as large of a damage interval as possible (an interval of at least 10.0 units (resistances must be accounted for) is needed to get a precision of at least 1% in the damage values) -- this ensured that the data would be good enough to draw accurate conclusions. The damage was only done to the shields, they where never allowed to drop below 25% since a bleed through into armor can happen that can mess with the observed damage numbers. Finally, the ships were positioned within optimal range and their speeds set to zero to ensure that the chance to hit is 0.50 = 100% and nothing less.
After 10,656 shots at the poor frigate, enough data was collected to make some conclusions about how the random damage distribution looks like. The data ends up in the My Documents\EVE\gamelogs folder (in Windows), and was easily copied into a prepared Excel sheet for analysis.
- Base damage
- The ammo type dealt: 7 EM and 5 Thermal
- The base damage on the lasers were: 24.9063
- Compensating for resistance (20% thermal) the modified base damage is: 22.8308
Analysis of the data and interpretation of some reduced frequencies of min and max results in the normal damage span:
Of the 10,656 shots the lowest recorded damage was 11.4 (recorded 15 times) and the highest non-perfect was 34.0 (recorded 33 times), perfect hits dealt 68.5 damage (recorded 101 times). On average, each damage number (anything between 11.5 to 33.9) was recorded 46.7 times (standard deviation = 7.02). The reason for the lower occurrences of the min and max results on normal hits comes from rounding effects. Any damage in-between has an interval of 0.1 units (22.2500 to 22.3499 both produce the 22.3 in the log). However the min and max values do not have that span. The lowest theoretical number is Base Damage × 0.5 = 11.415, hence the interval to get 11.4 in the log is between 11.415 and 11.4499, that is only 0.0345 difference. So the expected number of occurrences of the value 11.4 is only 34.6% of the average number, 15 recorded values / 34.6% = 43.4, close to average and inside the standard deviation. The upper interval is 67.8%, 33 times / 67.8% = 48.7, also close to average and inside the standard deviation. (Note: 34.6% + 67.8% = 102.4%, which is of course impossible—the error comes from rounding errors in the 4th decimal of the base damage, awesome precision isn't needed for this comparative calculation since the natural random deviation is much larger anyhow, so this is good enough, the objective was to explain the lower frequencies of the end points which now has been done).
- Lowest damage random multiple
- Modified base damage × 0.51 = 11.6
- Modified base damage × 0.50 = 11.4
- Modified base damage × 0.49 = 11.2
- The lowest observed damage is 11.4, thus 50%
- Highest non-perfect random multiple
- Modified base damage × 1.50 = 34.2
- Modified base damage × 1.49 = 34.0
- Modified base damage × 1.48 = 33.8
- The highest non-perfect damage is 34.0, thus 149%
- Perfect hits deal 68.5 damage
- Modified base damage × 3 = 68.5
The collected data shows that the normal damage is distributed within 50%–149%. Since the first 1% unit is used for critical rolls (this is most likely, if the last % unit was used additional calculations will be needed if the to hit chance is less than 1%), the constant added to the damage roll should be 0.49.
Turret grouping and damage
I did a test to verify that grouping has no effect on turret damage.
Shot at a ship inside optimal. Took damages for each shot from game log. Created quick histograms with MATLAB.
One turret has the flat distribution.
Three turrets grouped together form normal distribution. This is as expected with multiple separate random distributions together.
Hirmuolio pine (talk) 14:23, 19 December 2017 (CST)
