More actions
→Capacitor recharge rate: .png formula to <math> |
m indent math |
||
| Line 94: | Line 94: | ||
A player by the name of “Dust Puppy” investigated the recharge rate in-depth and published his findings<ref>[https://oldforums.eveonline.com/?a=topic&threadID=116993 Dust Puppy - Thoughts and research on the capacitor]</ref>. Based on his experiments, he suggests that the formula for calculating recharge rate is: | A player by the name of “Dust Puppy” investigated the recharge rate in-depth and published his findings<ref>[https://oldforums.eveonline.com/?a=topic&threadID=116993 Dust Puppy - Thoughts and research on the capacitor]</ref>. Based on his experiments, he suggests that the formula for calculating recharge rate is: | ||
<math> \displaystyle\frac{\text{d}C}{\text{d}t} = \frac{ 10C_{\rm{max}}}{T} \left( \sqrt{ \frac{C}{C_{\rm{max}}} } - \frac{C}{C_{\rm{max}}} \right) </math> | :<math> \displaystyle\frac{\text{d}C}{\text{d}t} = \frac{ 10C_{\rm{max}}}{T} \left( \sqrt{ \frac{C}{C_{\rm{max}}} } - \frac{C}{C_{\rm{max}}} \right) </math> | ||
...where:<br /> | ...where:<br /> | ||
| Line 108: | Line 108: | ||
The formula can be also used to write capacitor level as function of time | The formula can be also used to write capacitor level as function of time | ||
<math> \displaystyle C_1 = C_{\rm{max}} \left( 1 + e^{ \large 5 \frac{ t_0 -t_1 }{ T } } \left( \sqrt{ \frac{C_0}{C_{\rm{max}}} } - 1 \right) \right)^2 </math> | :<math> \displaystyle C_1 = C_{\rm{max}} \left( 1 + e^{ \large 5 \frac{ t_0 -t_1 }{ T } } \left( \sqrt{ \frac{C_0}{C_{\rm{max}}} } - 1 \right) \right)^2 </math> | ||
where C<sub>0</sub> is capacitor level at starting time t<sub>0</sub> and C<sub>1</sub> is capacitor level at time t<sub>1</sub> | where C<sub>0</sub> is capacitor level at starting time t<sub>0</sub> and C<sub>1</sub> is capacitor level at time t<sub>1</sub> | ||
Revision as of 11:40, 18 January 2020
Capacitor is the energy reserve your ship uses for everything. Without capacitor you can not activate modules so it is important to have enough energy in your ship.
Capacitor equipment
| High slot modules | |
| Remote Capacitor Transmitter allows a ship to transmit capacitor to a target ship. The target ship will receive more capacitor than the module consumes so in a fleet this module is used to generate more capacitor. | |

|
Energy Nosferatu is an offensive capacitor module. It does not use any capacitor but instead just leeches capacitor from the target ship. |
| Energy Neutralizer is an offensive capacitor module. Activating the module consumes capacitor but the target ship will lose even more capacitor. | |
| Medium slot modules | |
| Cap Battery increases the size of the capacitor pool by a flat ammount. Due to how capacitor recharge rate is calculated this will result in faster capacitor recharge. The module also gives partial resistance against hostile capacitor warfare. | |
| Capacitor Booster allows injecting more capacitor at demand. The module consumes cap booster charges. Each charge gives set ammount of energy. For example Cap Booster 200 will give 200 GJ of energy. | |
| Cap Recharger reduces capacitor recharge time. The result is faster capacitor recharge. | |
| Low slot modules | |
| Capacitor Flux Coil reduces the capacitor pool size and capacitor recharge time. Results in faster capacitor recharge but smaller capacitor size. | |
| Capacitor Power Relay Reduces capacitor recharge time resulting in faster capacitor recharge. But also reduces local shield booster boost ammount. | |
| * Power Diagnostic System offers small bonus to capacitor capacity and capacitor recharge time. | |
| Other | |
| |
| |
| Mindflood Booster gives a bonus to capacitor capacity. | |
| Antipharmakon Aeolis gives a bonus to capacitor capacity. | |
Skills
- Capacitor Emission Systems - 5% reduced capacitor need of energy transmitters and energy neutralizers. Only applies to subcapital modules.
- Capital Capacitor Emission Systems - 5% reduced capacitor need of capital energy transmitters and capital energy neutralizers.
- Capacitor Management - 5% bonus to capacitor capacity per skill level.
- Capacitor Systems Operation - 5% reduction in capacitor recharge time per skill level.
Capacitor recharge rate
- Your capacitor will recharge faster the closer you are to 25% of your maximum.
- The recharge rate drops of very quickly once you go below this.
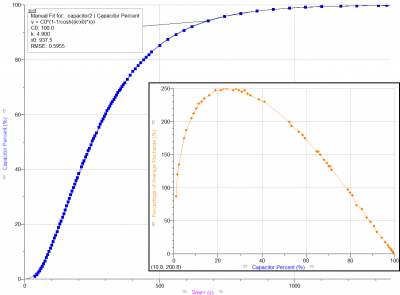
The capacitor recharge rate is a non-linear function—the rate at any given moment depends on how much energy is stored at that moment. Near zero and near full capacity, the recharge rate is very low, and it peaks at 25 percent.
The important thing to remember is that the recharge rate declines dramatically once it falls below 25% of capacity. Therefore, if in a fight, leave yourself a margin of safety and consider escaping if it appears that you will soon fall below this amount.
A player by the name of “Dust Puppy” investigated the recharge rate in-depth and published his findings[1]. Based on his experiments, he suggests that the formula for calculating recharge rate is:
...where:
C is your current capacitor level in GJ.
Cmax is your maximum capacitor level in GJ.
dC/dt is your current capacitor recharge rate in GJ/s. (Formally: The instantaneous rate of change of the capacitor charge C with respect to time.)
T is capacitor recharge time.
Capacitor recharge, therefore, peaks at 25%, and the advertised “Capacitor Recharge Time” is actually the time for the capacitor to go from dead empty to 98.7%, assuming no drains or boosts.
Experimenting with this formula,[2] it has been found that the peak recharge rate, without any effect of boosters or energy draining weapons, is indeed at 25% of capacitor capacity.
The formula can be also used to write capacitor level as function of time
- Failed to parse (unknown function "\large"): {\displaystyle \displaystyle C_1 = C_{\rm{max}} \left( 1 + e^{ \large 5 \frac{ t_0 -t_1 }{ T } } \left( \sqrt{ \frac{C_0}{C_{\rm{max}}} } - 1 \right) \right)^2 }
where C0 is capacitor level at starting time t0 and C1 is capacitor level at time t1
The full derivation may be found at http://forum.eveuniversity.org/viewtopic.php?f=222&t=30652 (dead link).
