| EVE University offers classes on: | |
The capacitor is an additional energy reserve that your ship uses to power modules and equipment that require a quick burst of energy.
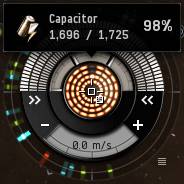
Overview
In many ways, your capacitor is analogous to the recharging pools of "mana" common in fantasy role-playing games. Just as in many games some spells and abilities require mana, certain modules and abilities in EVE require capacitor energy. Running out of mana means that you can't cast spells for a while; in EVE, running out of capacitor means that you can't use some modules for a while.
Modules
Every ship in EVE has an internal generator, which provides the "powergrid" you see in the fitting window. Modules fitted onto the ship connect to the powergrid and reserve a portion of the generator output for themselves, reducing the remaining powergrid when fitted.
Some modules require only connection to the powergrid to work: armor plates, damage controls, and weapon enhancers (gyrostabilizers, heat sinks, magnetic field stabilizers and ballistic control systems) for example. Most of these do not require player activation and are always working and players commonly call them "passive" modules. A few types of active modules, such as projectile turrets and missile launchers, must be activated by players but require only powergrid, not capacitor energy.
Some modules, however, need larger immediate bursts of power to operate. Energy turrets, for example, need energy to shoot destructive beams at your targets, while shield boosters and armor repairers use energy to replenish your defenses. These modules draw on the capacitor for their immediate energy needs. The capacitor permanently leeches a certain amount of generator output to charge itself up like a battery, or rather, like a real-life capacitor. When a module requires a quick burst of energy to operate, the capacitor discharges, providing that energy.
Travel
Your ship's warp engines use capacitor to initiate warp, and the amount of capacitor energy required depends on the warp distance. If you lack sufficient capacitor energy, your warp engines will take whatever is available, and warp you an equivalent proportion of the distance, dropping you out of warp somewhere between your departure point and destination.
Your ship's normal engines, used for movement in local space without warping, do not use capacitor, though popular additional propulsion equipment such as afterburners and microwarpdrives do. Jumping through a stargate or wormhole does not use capacitor.
Managing your Capacitor
Running dry
If your ship is completely drained of capacitor charge:
- You will not have enough energy to initiate warp.
- You will not be able to activate any active modules that require capacitor charge. You still can activate modules that do not, such as missile launchers.
Active, capacitor-using modules draw on the capacitor at the start of each cycle. A module that is already running will not stop working immediately when you run out of capacitor, but will instead run to the end of its current cycle and then switch off. So, for example, if you are running active shield hardeners that increase your shields' resistance to damage and you run out of capacitor, your hardeners will carry on running--and your shields will have increased damage resistance--to the end of their current cycle, and then stop.
Being drained of capacitor charge does not stop your engines or render your ship inoperable.
Merely fitting a microwarpdrive ("MWD") to your ship reduces the overall size of your capacitor, typically by 20–25% depending on the specific MWD module. This balances out the very high speed boost (around 500%) achieved when the MWD is activated. For many purposes, it is often worth fitting an MWD nevertheless, but this trade-off should be borne in mind.
The other common threat to your capacitor is capacitor warfare: hostile players or NPCs can use energy neutralizers to drain your capacitor energy away.
Ships' capacitor sizes tend to be within the same order of magnitude across similarly-sized and classed hulls, but they do vary. Amarr ships tend to have the largest capacitors because the most common Amarr weapon is energy-hungry laser turrets; Minmatar ships tend to have the smallest capacitors because none of their bonused weapons use capacitor at all.
Capacitor simulation
You can use the simulation function in the fitting window to simulate your capacitor's resilience in different situations. There is a tab for capacitor charge level simulation.
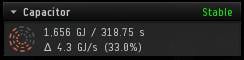
If a capacitor is '"stable", then even with every capacitor-consuming module running non-stop, your capacitor energy level will eventually drop down and fluctuate between the percentage level displayed, indefinitely, with the total drain on the capacitor balanced out by its recharge rate. Players often call a fit that runs with a stable capacitor "cap-stable".
If instead the window displays "Depletes in XX:XX", then with every capacitor-consuming module running non-stop, your capacitor energy level will drop to 0% after the displayed time.
Next to the orange circle display, four pieces of additional information are displayed. The top row is simply the max capacitor capacity and the recharge time. The bottom row is a bit more complicated. The "Delta" (Δ) of your capacitor indicates how resilient the capacitor will be under additional pressure beyond your current fit. It is (peak capacitor recharge rate) - (Max power consumption rate). Having a positive Delta means that your capacitor is stable. Having a greater positive Delta means that you can afford to be hit with additional capacitor loads and remain stable. Having a negative Delta means that your capacitor is not stable. Having a greater negative Delta means your capacitor depletes faster.
Stability
Although it is a good thing to be cap-stable, it is not a requirement in every situation. In some PvE and PvP combat situations, you will rarely need everything running at the same time, while in others stability is important. You must consider a fit's likely use and context.
Instead of compromising your ship's capability to force it to be cap-stable, you can sometimes achieve functional stability by managing your module use:
- Instead of running armor repairers or shield boosters non-stop, only activate them when you need to.
- Pulse a microwarpdrive for bursts of speed rather than letting it run permanently
- Keep your capacitor level above 25% at all times. Dropping below 25% drastically reduces its recharge rate.
- When facing enemies with energy neutralizers, try to keep your distance to reduce their effectiveness.
- If your ship is lacking in both capacitor stability and tanking ability, try to focus on mitigating damage and eliminating enemy targets quickly to avoid enduring the incoming DPS for long.
One type of mid-slot module, the "capacitor booster", uses ammunition to inject extra energy into your capacitor. A capacitor booster can keep an otherwise unfeasibly energy-hungry fit going, and can offer some protection against energy neutralizers. However, a capacitor booster will eventually have to reload, and even if you can survive the reload period, your cargo cannot hold unlimited charges for it. Cap-boosted fits can work well in some types of short, high-stakes PvP combat, but are usually ill-suited (and ISK-inefficient) in sustained PvE combat.
Capacitor recharge rate
Key points
The capacitor passively recharges from onboard generator power and requires no extra "fuel".
The capacitor recharge rate, in GJ per second, is based on the capacitor's capacity, the current capacitor charge, and its recharge time.
The capacitor recharges faster the closer it is to 25% of its capacity. At 95% or 5% capacity, it recharges relatively slowly; this is much more of a problem at 5% capacity! When a ship's capacitor has fallen below 25% capacity it usually struggles to recover if many modules are running, and players refer to this as the capacitor "breaking".
If you are flying a capacitor-dependent fit and your capacitor falls below 25% in the thick of combat, it is probably time to leave, if you can.
Mathematical details
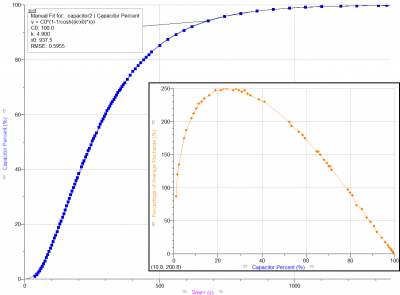
The capacitor recharge rate is a non-linear function—the rate at any given moment depends on how much energy is stored at that moment. Near zero and near full capacity, the recharge rate is very low, and it peaks at 25 percent.
The important thing to remember is that the recharge rate declines dramatically once it falls below 25% of capacity. Therefore, if in a fight, leave yourself a margin of safety and consider escaping if it appears that you will soon fall below this amount.
A player by the name of “Dust Puppy” investigated the recharge rate in-depth and published his findings[1]. Based on his experiments, he suggests that the formula for calculating recharge rate is:
...where:
- is your current capacitor level in GJ.
- is your maximum capacitor level in GJ.
- is your current capacitor recharge rate in GJ/s. (Formally: The instantaneous rate of change of the capacitor charge with respect to time.)
- is capacitor recharge time.
Capacitor recharge, therefore, peaks at 25%, and the advertised “Capacitor Recharge Time” is actually the time for the capacitor to go from dead empty to 98.7%, assuming no drains or boosts.
Experimenting with this formula,[2] it has been found that the peak recharge rate, without any effect of boosters or energy draining weapons, is indeed at 25% of capacitor capacity.
The formula can be also used to write capacitor level as a function of time:
where is capacitor level at starting time and is capacitor level at time
Capacitor equipment
| High slot modules | |
| Remote Capacitor Transmitter allows a ship to transmit capacitor to a target ship. The target ship will receive more capacitor than the module consumes, so in a fleet this module is used to generate more capacitor. Remote capacitor transfer counts as a form of remote assistance, and a ship using it will therefore inherit its target's aggression status, timers, and engagement flags. | |

|
Energy Nosferatu is an offensive capacitor module. It does not use any capacitor but instead just leeches capacitor from the target ship. |
| Energy Neutralizer is an offensive capacitor module. Activating the module consumes capacitor but the target ship will lose even more capacitor. | |
| Medium slot modules | |
| Cap Battery increases the size of the capacitor pool by a flat amount. Due to how capacitor recharge rate is calculated this will result in faster capacitor recharge. The module also gives partial resistance against hostile capacitor warfare. | |
| Capacitor Booster allows injecting more capacitor at demand. The module consumes cap booster charges. Each charge gives a set amount of energy. For example, Cap Booster 200 will give 200 GJ of energy. | |
| Cap Recharger reduces capacitor recharge time. The result is faster capacitor recharge. | |
| Low slot modules | |
| Capacitor Flux Coil reduces the capacitor pool size and capacitor recharge time. Results in faster capacitor recharge but smaller capacitor size. | |
| Capacitor Power Relay Reduces capacitor recharge time resulting in faster capacitor recharge. But also reduces local shield booster boost amount. | |
| Power Diagnostic System offers small bonus to capacitor capacity and capacitor recharge time. | |
| Other | |
| |
| |
| Mindflood Booster gives a bonus to capacitor capacity. | |
| Antipharmakon Aeolis gives a bonus to capacitor capacity. | |
Skills
General
- Direct capacitor-related skills:
- Capacitor Management - 5% bonus to capacitor capacity per skill level.
- Capacitor Systems Operation - 5% reduction in capacitor recharge time per skill level.
- Warp:
- Warp Drive Operation - 10% less capacitor needed to initiate warp per level.
Training Capacitor Management, Capacitor Systems Operation and Warp Drive Operation to IV is a good thing to do for relatively new pilots, as doing so is relatively quick and offers substantial benefits to every ship. Training the first two to V is a good long-term goal, and having Warp Drive Operation at V is nice though less important.
Module-specific
The following skills benefit commonly-used modules, making them valuable training choices:
- Afterburner - 5% reduction to Afterburner duration and 10% reduction in Afterburner capacitor use per skill level.
- High Speed Maneuvering - 5% reduction in Microwarpdrive capacitor usage per skill level.
- Controlled Bursts - 5% reduction in capacitor need of weapon turrets per skill level.
- Propulsion Jamming - 5% Reduction to Warp Scrambler, Warp Disruptor, and Stasis Web capacitor need per skill level. This is a valuable skill for a lot of PvP combat.
- Shield Compensation - 2% less capacitor need for shield boosters per skill level.
Controlled Bursts is not important if your favored weapons systems are missiles, projectile turrets, or drones, which do not use capacitor. This skill is therefore irrelevant to flying Minmatar ships, and less useful for some Gallente drone ships and Caldari missile ships. Propulsion Jamming is more important for PvP pilots and less important for PvE pilots.
The following skills benefit less universally-used modules, but will be relevant to some pilots:
- Capacitor Emission Systems - 5% reduced capacitor need of energy transmitters and energy neutralizers. Only applies to subcapital modules. This skill is useful for capacitor warfare.
- Electronic Warfare - 5% less capacitor need for ECM and ECM Burst systems per skill level. Useful for Caldari electronic warfare.
- Sensor Linking - 5% less capacitor need for sensor boosting and sensor dampening per skill level. Useful for Gallente electronic warfare.
- Target Painting - 5% less capacitor need for target painters per level. Useful for Minmatar electronic warfare.
- Weapon Disruption - 5% less capacitor need for weapon disruptors per skill level. Useful for Amarr electronic warfare.
The following skills are primarily relevant to capital ships, and therefore not immediately relevant to new players:
- Jump Drive Operation - 5% reduction in capacitor need of initiating a jump per skill level.
- Capital Capacitor Emission Systems - 5% reduced capacitor need of capital energy transmitters and capital energy neutralizers. Only applies to capital ship modules.
Capacitor gauge
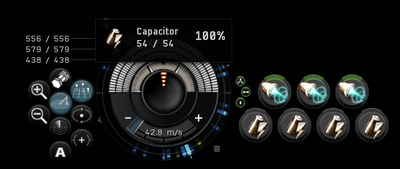
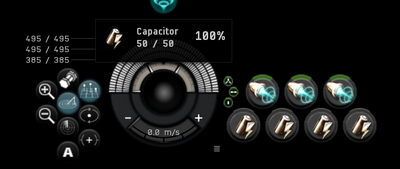
Your capacitor gauge is made up of many fragments that can split into four parts each. The number of fragments is determined by your capacitor capacity.
For every 50 GJ of capacity your ship has, one fragment is added to the gauge, until the maximum of 18 is reached. A full gauge with 18 fragments needs 900 GJ of capacity to appear. However, the capacitor gauge in the fitting window can only show up to 10 fragments.
If you managed to get your capacitor capacity below 50 GJ, via fitting a Microwarpdrive or Capacitor Flux Coil to all slots, your capacitor gauge will disappear as it has 0 fragments.
| Fragments | Least capacity |
|---|---|
| 1 | 50 GJ |
| 2 | 100 GJ |
| 3 | 150 GJ |
| 4 | 200 GJ |
| 5 | 250 GJ |
| 6 | 300 GJ |
| 7 | 350 GJ |
| 8 | 400 GJ |
| 9 | 450 GJ |
| 10 | 500 GJ |
| 11 | 550 GJ |
| 12 | 600 GJ |
| 13 | 650 GJ |
| 14 | 700 GJ |
| 15 | 750 GJ |
| 16 | 800 GJ |
| 17 | 850 GJ |
| 18 | 900 GJ |
