More actions
text math into <math> |
I really mangled the synthesis of the previous sections when I added the intro. This should make it clearer what the exponential is and what the conventions for a hit are, in-line with previously written info prior to may 2019. |
||
| Line 6: | Line 6: | ||
== Synopsis and number generation == | == Synopsis and number generation == | ||
The ''hit chance'' is an exponent expression that gives an accuracy percentage based on two terms, tracking and range: the closer the terms of the exponent are to zero, the better the chance of a hit, because when plugged back in to the exponent, anything raised to zero instead becomes 1.00 or 100%. This exponent and the two terms are fixed by the physical ships involved. The value of this expression sets a threshold for the following step. | |||
Secondly, the game generates a random number of some precision between 0 and 1. This number is used in both of the following equations, '''hit math''' and '''base-damage coefficient'''. The random value is used twice: it has to be ''under'' the threshold established by the hit chance expression in order to hit, but high enough to cause good damage. | |||
The ''base damage coefficient'' is the random number added to 0.49, and serves to adjust the "damage caused" number given in the fitting window (which is in turn the ammunition damage scaled by the turret's damage multiplier). This coefficient can vary from 0.50 to 1.49 of "damage caused" or 3.0 in a special case. In the following sections, these two numbers and their equations will be explored in greater detail. | |||
=Hit chance= | =Hit chance= | ||
| Line 167: | Line 171: | ||
===Average damage=== | ===Average damage=== | ||
As was mentioned earlier, your chance of dealing good, more damaging hits (' | As was mentioned earlier, your chance of dealing good, more damaging hits ('smashing' shots that deal more damage) decreases as your chance to hit decreases. This relationship is not linear, and your chance of good hits decreases quite rapidly as you move into falloff. At optimal + falloff, where your chance to hit is (as always, assuming other factors don't intervene) 50%, you can expect 40%, not 50%, of your theoretical maximum DPS. | ||
A turret with a hit chance of 100% will strike for 50% - 149% of its base damage with every non perfect hit. But when the hit chance is reduced, the upper random damage interval will also be reduced. The average damage is thus reduced in two ways, firstly by having some shots miss completely and deal no damage at all, and secondly by having the maximum random damage go down. The average damage will therefore always be reduced more than the hit chance is. | A turret with a hit chance of 100% will strike for 50% - 149% of its base damage with every non perfect hit. But when the hit chance is reduced, the upper random damage interval will also be reduced. The average damage is thus reduced in two ways, firstly by having some shots miss completely and deal no damage at all, and secondly by having the maximum random damage go down. The average damage will therefore always be reduced more than the hit chance is. | ||
Revision as of 21:43, 12 February 2020
| Weapon Systems |
|---|
|
|
|
|
|
|
| Other Weapon Systems |
| Other Mechanics |
Turret mechanics dictate how accurately turrets hit and how much damage is dealt. It is obvious that these two are connected since missing shots directly affects applied damage but the hit and damage mechanics are actually connected in another way too.
There are basically two things that affect your chance to hit a target with a turret-mounted weapon: range and tracking. This guide explains each factor in turn, and explores some of these factors' practical implications for combat. The second section looks at how the damage is calculated and how hit chance effects damage distribution. having a basic understanding on the mechanics is important for anyone who flies a turret based ship in EVE, or wishes to avoid being hit by 1400mm artillery fire.
Synopsis and number generation
The hit chance is an exponent expression that gives an accuracy percentage based on two terms, tracking and range: the closer the terms of the exponent are to zero, the better the chance of a hit, because when plugged back in to the exponent, anything raised to zero instead becomes 1.00 or 100%. This exponent and the two terms are fixed by the physical ships involved. The value of this expression sets a threshold for the following step.
Secondly, the game generates a random number of some precision between 0 and 1. This number is used in both of the following equations, hit math and base-damage coefficient. The random value is used twice: it has to be under the threshold established by the hit chance expression in order to hit, but high enough to cause good damage.
The base damage coefficient is the random number added to 0.49, and serves to adjust the "damage caused" number given in the fitting window (which is in turn the ammunition damage scaled by the turret's damage multiplier). This coefficient can vary from 0.50 to 1.49 of "damage caused" or 3.0 in a special case. In the following sections, these two numbers and their equations will be explored in greater detail.
Hit chance

The basic question of shooting a turret is whether you will hit or not. In EVE, hitting with a turret is not quite a simple question of being either in range or out of range. Instead it depends on the concepts of optimal range, falloff and tracking. You can find figures for all of these if look at your fitted turret info.
Due to how the hit chance is calculated the range and tracking do not affect each other and can be considered separately. A nice thing to remember is that against a stationary target the tracking part can be ignored while against a target that is in optimal range the range part can be ignored.
Range
Every turret has two range parameters called "Optimal Range" and "Accuracy Falloff".
A gun's optimal range is the range within which distance has no effect on hit chance. In other words in optimal range the distances can be completely ignored and only tracking has any effect on hitting.
Accuracy falloff begins at the end of optimal range. Falloff measures how quickly the chance to hit decreases as the target distance grows beyond optimal range. At a gun's optimal range plus its falloff, the chance to hit is reduced to 50%. At a gun's optimal range plus twice the falloff range, the chance to hit is reduced to only 6.25%. Since other factors can reduce this hit chance even further, at excessive ranges it is often not worth it at all to fire turrets, unless you're trying to draw aggression from a rat (which can be done at maximum targeting range).
So, for example, you're firing a gun which has 20km optimal range and 6km falloff at a target which is moving steadily straight away from you (zero transversal), starting at only 1km range. You will (if nothing else intervenes) always hit a target that is less than 20km (your optimal range) from you; your chance to hit will gradually decrease as your target moves between 20km and 26km (your optimal + falloff) from you, reaching 50% at 26km. By 32km (optimal + twice your falloff) your chance to hit will be down to 6.25% and decreasing.
The penalty for exceeding the optimal range by a small amount is reasonably low; the chance to hit a target at 33% of the falloff range in excess of the optimal range is still above 90%. Minmatar ships especially have significant falloff ranges allowing them to fight effectively beyond their optimal range. However, as the distance increases, the chance to hit decreases faster and faster.
When using turrets that fight inside falloff ranges it can be useful to know that being at optimal+(falloff / 2) results in -20% average damage and being at optimal+falloff results in -60% average damage (note: average damage falls faster than hit chance due to how the random damage interval is calculated, see below).
Falloff and optimal ranges are visible in the turrets info window. They are further modified by skills, ammo, modules, hull bonuses and incoming tracking disruptors. Target distance is visible on the overview.
Tracking
Tracking tells how well turrets hit a moving target. If the target is stationary relative to the shooter tracking is ignored and only range effects hit chance. If the target is both inside optimal range and stationary the turrets have 100% chance to hit. As a result against stationary target the turret tracking is irrelevant and even the largest turrets can hit the smallest targets if the target is foolish enough to sit still.
This is why it is possible for a rack of battleship guns to hit a frigate for (as they say) massive damage despite the frigate's very small signature: if the frigate sits still, or burns straight towards or away from the battleship, or is at a long enough range that despite its speed it doesn't have much angular velocity from the battleship's point of view, it is toast.
Against moving targets the tracking is more complicated concept than range due to larger number of variables, less intuitive variables, the player not seeing all the variables and chaotically changing variables. Tracking depends on three variables: "Turret Tracking", angular velocity and target signature radius.
The concept of turret tracking value is simple: The smaller a turret is, the faster its tracking speed will be: small autocannon, for example, track faster than medium autocannon. Short-ranged varieties of turret have better tracking than their long-ranged counterparts -- so, for example, medium pulse lasers track faster than medium beam lasers and large blasters track faster than large railguns. There is only one value for tracking unlike the optimal and falloff for range. One way to look at it is to consider the turret to always being in "tracking falloff" with zero optimal tracking.
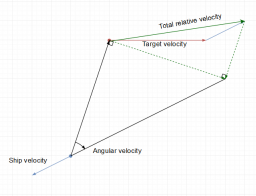
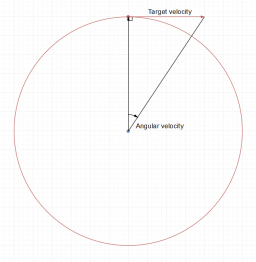
Instead of measuring an object's speed as m/s or miles/hour, a speed can also be measured as an angle. A good example is the suns movement across the sky, where it moves 360° in 24 hours, which makes the angular velocity 15°/hour. If the sun is moving away or towards us wouldn't matter, because that wouldn't change the angle, only sideways movement counts.
Just as a circle can be described as an angle of 360°, it can also be described as an angle of 2π radians. Meaning that one radian equals to roughly 57° (360/2π).
The ingame overview can show the angular velocity of a target if you open the settings and tick a box under the tab called columns. Angular velocity is used to determine the penalty to the hit chance based on the turret's tracking ability. Relying on high angular velocities to stay alive is called speed tanking (not to be mixed up with kiting, which is to keep something at range).
Angular velocity is calculated as ω=vt/d, where vt is transversal velocity of the target relative to shooter and d is distance to target. Two ships will always have the same angular velocity to each other.
Angular velocity depends on the ratio of transversal velocity and range (it's to do with the geometry of circles and radii) -- but it's easier to think about angular velocity since measurements of it in radians per second relate easily to the figures for gun tracking speed.
In chance-to-hit calculations, your guns' tracking speed is compared against your target's angular velocity and signature radius. Angular velocity is a geometric concept to do with radii of circles, but it can be hard to visualize. One way to think about it is to imagine that your screen's point of view in EVE is looking out above the barrels of your turret as it looks at your target -- a turret's-eye-view, so to speak. If your target was moving quickly across your turret's point-of-view, it would have a high angular velocity, and if it was moving slowly across your turret's point-of-view it would have a low angular velocity. Due to symmetry the angular velocity is same for both ships.
The ratio of your target's angular velocity to your guns' tracking speed is what's important. If their angular velocity is high, the ratio will be high, and you're very unlikely to hit them. The speed at which a target moves across a turret's field of view doesn't depend only on the target's real velocity. The direction the target's moving in relative to the ship firing at it matters too: a ship that burns straight towards you could be quite easy to hit, regardless of its speed, because it's not moving very fast across your turrets' point-of-view. Range also affects angular velocity: a target orbiting you at 400m/s at a range of 7,000m has a much higher angular velocity than a target orbiting you at 400m/s at a range of 30km.
Lastly the target signature radius. Every ship in EVE has a signature radius (you can find a figure for yours on the fitting screen). Signature radius represents, roughly speaking, a ship's footprint on everyone else's sensors. This can be thought of as multiplier that is applied to the ratio of angular velocity and turret tracking.
Signature radius depends mostly on hull but target painters and many shield modules will increase it. Some examples of ship signature radiuses without modules:
- Tormentor 35 m
- Thrasher 56 m
- Caracal 125 m
- Brutix 305 m
- Tempest 360 m
As the ratio (tracking*signature radius)/angular velocity is the important part you can see clearly how much easier larger ships are to hit. Against a battleship you can go 10x faster than against a frigate while still enjoying same hit chance, or in other words you must somehow slow down a frigate to 1/10th of the speed of a battleship to hit it with same accuracy as if it was a battleship.
Due to how nice ratios are doubling tracking, doubling target signature radius and halving angular velocity all have exactly same effect on hit chance. This makes it very easy to hit large targets at high speeds and also makes webs and manual piloting very effective at manipulating hit chance as seen in sections below.
Since the tracking depends on all three: target signature radius, turret tracking and angular velocity it can be hard to intuitively see when it is possible to hit. For example a medium autocannon with 50 tracking shooting a cruiser with 150 m signature radius and an angular velocity of 0.073 rad/s has 90% chance to hit. In same situation, but when shooting at frigate with 50 m signature, the hit chance is only 39%.
| Hit chance from tracking | Angular velocity (rad/s) as a function of tracking (T) and signature radius (S) |
|---|---|
| 50% | T×S/40000 |
| 60% | T×S/47000 |
| 70% | T×S/56000 |
| 80% | T×S/70000 |
| 90% | T×S/103000 |
| 100% | 0 |
It is often best to use a Third-party tools to see how well your guns track moving targets. Both EFT and PYFA are able to draw damage application figures on moving targets.
Much of this information is most useful when theorycrafting, as there is often little time or need for complex mathematics during combat. However, pilots who are familiar with these concepts can still use them in a general sense to make decisions when in space.
| A long, long time ago... |
|---|
| Updates to tracking have made it much easier to compare the tracking abilities of different turrets, but they have also made the numbers more abstract and harder to use in combat (not that it was feasible to compare tracking numbers before unless fighting targets of same size). The "Turret Tracking" attribute in the formula used to be split into "Turret Tracking" and "Turret Signature Resolution". Combining them to single number simplified the formula without changing any mechanics. If you need to calculate turret hit chance with "Turret Signature Resolution" (for example using old NPC attribute info) just replace 40000 with Turret Signature Resolution. If you encounter nonsensical tracking values anywhere they may be in this old format.
To convert turret tracking speed to rad/s the following formula can be used: turret tracking (new) = Turret tracking (old) * 40000 m / Optimal Signature Resolution |
Hit Math
A turret's chance to hit a target is calculated using the equation below. It will produce a result between 0 and 1, representing a probability between 0% and 100%. This value is then compared to a random number between 0 and 1. If the random number is greater than the calculated result, the turret misses.
Note: The entire expression contained within the outermost set of parentheses is an exponent.
- Failed to parse (unknown function "\Large"): {\displaystyle \displaystyle\text{Chance to hit} = 0.5^{\Large \left( \left( \frac{\text{Angular} \times 40000 \text{ m}}{\text{Tracking} \times \text{Signature}} \right)^2 + \left(\frac{\max(0,\ \text{Distance} - \text{Optimal})}{\text{Falloff}} \right)^2\right)}}
Angular is the angular velocity (movement between the attacker and the target expressed as an angle in radians per second).
Tracking is the turret's tracking value (listed on the info window and means how well the turret can hit a moving target).
Signature is the target signature radius (aka target size, a big target is easier to track).
Distance is the range in meters.
Optimal is the optimal range of the turret.
Falloff is the falloff range of the turret.
The hit chance equation has the form of x(a+b), which can also be written as xaxb. In this case, x = 0.5, a = all tracking terms and b = all range terms. In other words, the hit chance equation can be thought of as having two separate parts (tracking and range), which are calculated individually and then multiplied at the end to get the final hit chance. This means that tracking and range don't interfere with one another, they are indeed two separate things.
The equation also shows that the reduction of hit chance from falloff and tracking respectively follow the same pattern. This is because they both look like 0.5(something / x)2, where x is either tracking or falloff. The only difference between them are the input variables, the output look the same.
The equation is not fully realistic, as it only considers the relative movement between the attacker and the target, and does not take into account any rotation of the attacking ship. From the attacker's point of view, this relative movement appears as a change in the angle to the target.
Example: At a range equal to optimal+falloff the range part of the equation becomes 0.51, which means a 50% chance to hit. Against a target with the same angular velocity (rad/s) as a turrets tracking value multiplied with the targets size and divided by 40000m, the tracking part of the equation becomes 0.51, which is also a 50% chance to hit. In the first case the full falloff range was used, in the second case the full turret tracking was used, and since they both follow the same pattern they end up at the same hit chance.
Damage
The damage that a turret deals will be randomly spread around a fixed value called base damage. The base damage is calculated from the turret's Damage Multiplier attribute, the ammo's damage values, hull modifiers and skills. The base damage is the so called "paper damage" that is shown in all info windows. "Paper DPS" is simply "paper damage" divided by rate of fire.
But the surprising part of the damage mechanic is that the damage calculations are linked to hit chance calculations. At the heart of each turret's damage output is a single randomly generated value between 0 and 1 that is several digits long. This random number is used to determine both if the turret hits and how much damage it does. Unfortunately, the misses are those random numbers that would have caused the most damage. If the random number is less than 0.01 (1% chance) a special case occurs, a perfect hit, these will always deal exactly 300% of the base damage. A funny result of this is that when the hit chance is 1% or less, only misses and perfect hits can occur.
The damage modifier for a normal hit is calculated with the following formula. In 100% hit chance situation this leads to even distribution from 50% to 149% with extra spike at 300% damage.
The normalized DPS, that takes both hit chance and random damage variation into account, can then be calculated as
The combat log will show the quality of a hit as follows
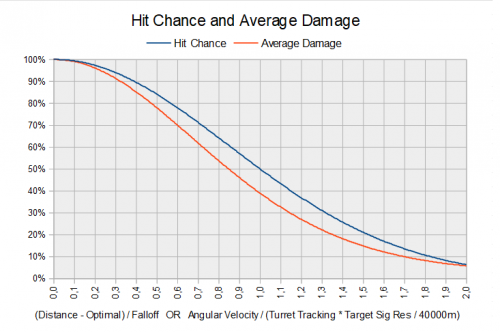
| Hit description | Random damage modifier |
|---|---|
| Grazes | 0.500–0.625 |
| Glances off | 0.625–0.750 |
| Hits | 0.750–1.000 |
| Penetrates | 1.000–1.250 |
| Smashes | 1.250–1.490 |
| Wrecks | 3.000 |
Average damage
As was mentioned earlier, your chance of dealing good, more damaging hits ('smashing' shots that deal more damage) decreases as your chance to hit decreases. This relationship is not linear, and your chance of good hits decreases quite rapidly as you move into falloff. At optimal + falloff, where your chance to hit is (as always, assuming other factors don't intervene) 50%, you can expect 40%, not 50%, of your theoretical maximum DPS.
A turret with a hit chance of 100% will strike for 50% - 149% of its base damage with every non perfect hit. But when the hit chance is reduced, the upper random damage interval will also be reduced. The average damage is thus reduced in two ways, firstly by having some shots miss completely and deal no damage at all, and secondly by having the maximum random damage go down. The average damage will therefore always be reduced more than the hit chance is.
Example: When the hit chance of a turret is 70% the damage interval has shrunk to 50% - 119% for all non perfect hits. When combined, these two things results in an average damage of just 61.3% (69%*(50%+119%)/2+1%*3) of the base damage.
Will grouping guns change the damage?
No. Even if the guns are grouped on your screen, they are still treated separately. This can be seen by collecting damage data and comparing that with the expected damage distribution, it's very clear that it's a combination of several separate turret shots instead of a single one. It can also be deduced by looking at the turret group's damage output when shooting at hard to hit objects, like things deep into falloff, it's then possible to tell when one, two or more guns hit the target.
Practical applications
The hit chance and its relation to range, tracking, velocity and signature radius have many effects on combat with turret ships. Taking advantage of this knowledge allows you to control range, control velocities and choose the right modules for the job. This section gives several useful tricks and maneuvers for ships that either fight with turrets or against a turret ship.
Although you can add angular velocity (or transversal velocity, if you want it) as an extra column to your overview, you'll never have the time in combat to get out a calculator and run through chance-to-hit equations. There are however some tactics which let you use gunnery mechanics to your advantage.
Most turrets lose their effectiveness fast outside optimal range. Autocannon are an exception here, as they have very long falloff ranges and some Minmatar ships have specific bonuses to falloff (220mm autocannon loaded with Barrage and fitted on a Vagabond with Tracking Enhancers can theoretically have over 40km falloff, for instance). Pilots flying with autocannon should therefore feel happier about fighting in falloff.
Obviously if you find a way to pin your enemy down at a range where you can hurt them but they can't hurt you, you'll win. On the other hand, if you find yourself fighting an enemy who outranges you and can move faster than you, and you can't ameliorate either of those problems, you should consider trying to escape.
Although you can use tools like EFT's DPS graphs, this knowledge comes partly with experience. It's much easier to figure out against NPC rats, which always have the same characteristics while kindly heading more or less straight for you until they close into their preferred orbit range, than it is with PvP enemies.
But range control is not the end of turret management. You must also always remember that range is directly tied to angular velocity. In practice, if you're using long-ranged turrets (artillery, railguns and beam lasers) you will find that once targets get close enough within your optimal range their angular velocity will rise so much that you can't hit them. Some ways to handle small, fast, closely-orbiting targets are discussed below. Besides dealing with them once they do get close, it's worth finding a range which is within your optimal yet far enough away that the enemy are easy to track.
If your ship is faster and more agile, and the opponent is orbiting you, the angular velocity can be minimized (can reach zero) by using Approach. If your ship is slower or less agile, and the opponent is orbiting you, angular velocity can be minimized by using Keep at Range (if set to far away, but be warned: if you reach this range your ship will stop). Alternatively, if your ship has very poor agility, it is better to fly in a straight line to maximize your own speed and let the orbiting ship chase after you. Maximizing the angular velocity is harder but will happen if both ships orbit one another, or if one is using Approach but isn't agile enough to get behind the other. A ships agility is the multiplication of its inertia modifier and mass, a lower value means it can do sharper turns.
In missions with slow battleship and dumb AI you can look at the velocity vector of your target either with tactical overlay or by looking at their ship model. You can then easily attempt to match velocity vector with them by manually aligning in same direction they are going. If the speed and velocity vector are matched angular velocity drops very low and hitting is much easier.
From the point of view of a large ship struggling to hit small fast ships which are orbiting close to it, either in PvP or PvE, the solution is to reduce your target's angular velocity and/or increase their signature. If you can almost entirely reduce their angular velocity you won't need to worry about increasing their signature because (as described above) the effects of signature radius and resolution affect the tracking calculation within the chance to hit calculation, not the chance to hit calculation directly. Stasis Webifiers are a common solution. T1 webs reduce their target's speed by 50%, T2 webs by 60% (overheating a webifier increases its range, which can help you snag a player who's dancing just beyond web range). Target Painters will help, though it is not as effective as web it has much greater range. You can also try boosting the tracking speed of your guns with Tracking Computers and Tracking Enhancers.
There are rigs and modules that improve tracking directly. However, since bigger targets are easier to track, a Target Painter will also make someone easier to track. A Target Painter is an active module and will require more micromanagement of its pilot, but the good thing is that the victim is easier to track for everyone.
Shield extenders increases the signature resolution (size) of a ship, which makes them easier to track with turrets. Armor plates increases mass (slower turn speed) and reduces the top speed with afterburners and microwarp drives, which makes them easier to track too.
Controlling battle
The conclusion from all the information about tracking speed and signature radius is: when you want to avoid damage, you want your angular velocity to be as high as possible and your signature radius to be low. But if you want to hit should probably try to fight within your guns' optimal range, but be prepared to fight within your optimal + falloff range (also called 'first falloff') if you must. One of the simplest yet important rules to remember is that two ships always have the same range and angular velocity towards eachother. The pilot who can control these two values, can control how much damage turrets will be able to do.
If the size and speed difference between you and your target is not so great, you may be able to reduce their angular velocity simply by maneuvering.
- You can try burning away from them -- hopefully encouraging them to follow you in a straight line.
- If they're not chasing you directly you can try burning on a course parallel to theirs and in the same direction, which should also reduce angular velocity.
- If they're trying to keep beyond a particular range (web range, for example) from you, you can try burning straight towards them -- they may make the mistake of burning directly away from you along the course you're traveling.
- If you're fighting a player who's trying to keep outside of web range, but has to stay within the range of a long point to keep you tackled, you can try burning away to get them to chase you, and then turning around and burning towards them -- at least this will disrupt their orbit, and at best you will trick them into web range (again, remember that overheating increases web range).
If you have a PvP fleet of large ships that are struggling to hit a swarm of smaller targets you may find it helpful to spread out, and order each ship to target the enemies furthest away from it. Even if your enemies are flying under your guns individually, you can use the low angular velocity provided by greater range to kill the small ships attacking your fleetmates, who can do the same to the small ships attacking you. (By the same token, large ships are most vulnerable to smaller enemies when they're on their own.)
However, if you're in a ship that is very much larger and slower than your target, you're unlikely to be able to win through good manual piloting. Sometimes, however, the solutions to this problem aren't directly related to gunnery. battleship fits usually outsource frigate problems to drones. In PvP larger ships can use drones, large energy neutralizers, smartbombs or the help of smaller support ships to drive small, fast targets off or kill them.
For new pilots who are likely to be flying small fast ships one of the key ideas that follows from this is the tactic of 'flying under the guns' of an enemy ship: orbiting them at high speed and short range so it's very hard for their guns to track your small-signature ship. (Sometimes referred to as a form of 'speed tanking' or 'sig tanking'.) Assuming you're fast and small enough to survive under the enemy's guns, the main trick is getting there in the first place: if you burn straight towards the enemy, they will probably hit you (especially if you have an active MWD). If you approach a distant target straight on, there is no angular velocity, and the hit chance from the tracking term will be 100%. A battleship can easily hit a frigate for full damage if there is no need to track it.
Therefore it's wise to spiral in towards the enemy. To do this:
- Zoom in reasonably close to your ship and press C to make your camera autofollow the selected enemy (alternatively center the camera on your enemy manually so that it covers up the enemy on your screen.)
- Now double-click in space halfway between your ship and the edge of the screen (in any direction).
- Your ship will begin moving roughly towards the enemy, but not directly at them; it will also move away from its position covering the enemy ship on your screen.
- As it does so, every few seconds repeat double-clicking halfway between your ship and the edge of your screen. (If you are playing without autocamera repeatedly realign your camera so your ship goes back to blocking your view of the enemy, and each time you do so double-click halfway between your ship and the edge of your screen again.)
- This should make you spiral around them, moving ever closer until you can orbit (hopefully safely).
- There is no six. (It burned straight towards the enemy with its MWD on and was one-shotted.)
- It might be a good idea to practice this on large NPC belt rats before trying it in PvP combat.
Similarly it's good not to just burn straight away from a larger enemy if you're trying to escape, though by that point in a battle you may find you're too busy to take account of your relationship to enemy tracking. To do this spiral out:
- Open the Tactic overview (which is located left to your HUD, or press CTRL + D)
- Make sure you have the ship selected from which you want to escape
- Zoom in reasonably close to your ship, notice the line drawn between the enemy and your ship.
- Then turn your camera by about 180° and try use that line to look directly away from the enemy (don't bother with matching the line perfectly)
- Now double-click in space halfway between your ship and the edge of the screen (in any direction).
- Six shan't be.
- Repeat realigning your camera to the line and then repeat double-clicking.
The Disruption EWAR module will reduce a turrets tracking and/or range. Since ships are often fitted around an idea, like fighting at a certain range, a disruptor can really mess with that. Always bring both range and tracking disruption scripts, you won't know which one you'll need until you are in combat.
Caveats
- Against missile ships angular velocity is irrelevant, although a small signature and high speed still help you reduce damage from missiles; if you're only facing a missile ship, you could head straight for them
- Drone ships using normal drones (not sentry drones) won't have a problem because their main damage dealing is coming from the drones, not any guns they have fitted
- Your angular velocity will be different in relation to different people: if you're safely orbiting one enemy fast and close enough that he can't hit you, another enemy who's 20km away might be able to hit you much more easily
- When you finally issue an orbit command to your ship it may change direction, possibly one which will briefly, but dramatically, reduce your angular velocity; there's a lower chance of this happening if you issue the orbit command before you reach your planned orbit range, rather than once you're already within it
- Your orbit will probably not be circular, but elliptical, with your angular velocity rising and falling as you travel around it
- If you orbit very close to your target, your ship will fly an elliptical orbit to try to cope with the fact that your speed makes it hard for it to fly a tight orbit (afterburners will exacerbate this)
- If your target is moving (and it probably will be) this will also produce an elliptical orbit
- Your enemy may have smartbombs, and medium and especially large smartbombs deal quickly with frigates; this is why rookie tacklers are advised to orbit large ships outside smartbomb range
References
https://www.reddit.com/r/Eve/comments/5h24bk/turrets_listed_signature_resolution_is_40km/
